引言
在以往的博文中,我们介绍了深度学习。深度学习是一种通过多层神经网络实现自动化特征提取,从而实现图像识别、语音识别、自然语言处理等目的。
与深度学习不同,强化学习是一种通过智能体与环境的交互来学习最优策略的方法。举一个简单的例子:
让机器人走这个赛博迷宫
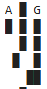
A表示机器人现在的位置,S表示起点(A目前就在起点),G表示终点,█表示墙。如果机器人撞了墙,我们就给它点惩♂罚;如果机器人走到了终点G,我们就给它奖励;当然,为了防止机器人原地踏步,我们定义每走一步都要接受一点小小的惩罚(不过这个惩罚远小于撞墙惩罚)
我们定义损失函数为惩罚,去优化这个模型,最后得到的效果必然是机器人不撞墙的走到终点。这个模型就是一个强化学习的模型。
虽然我们之前研究过使用BFS走迷宫,但是我们还可以使用更高级的强化学习方法,通过机器人与环境的交互,让机器人自我学习如何走迷宫,实现解决走迷宫这个问题。
对于机器学习,我们通常需要建立数学模型,然后迭代训练以最小化损失。强化学习也类似,我们先建立马尔可夫决策过程数学模型,并使用强化学习通过反复尝试来寻找最优策略。
马尔可夫决策过程(MDP)
所谓“马尔可夫决策过程”,就是Markov Decision Process(MDP),简单的来说就是:
在某种情景下,我们需要连续的做出决策,而且每个决策会带来一定的结果和新的状态。
例如机器人走迷宫,需要连续的做出往哪个方向走的决策,每个决策会产生不同的后果(撞墙受惩♂罚,原地踏步受小惩罚,到终点得到奖励),而且每个决策后,会使机器人到达新的状态(机器人位置变了)。
MDP的四个关键要素是:状态(State)、动作(Action)、奖励(Reward)和转移概率(Transition Probability)
- 状态:状态是描述当前情景的信息,在机器人走迷宫的例子中,状态就是机器人当前的位置、当前的奖励/惩罚值。
- 动作:在每个状态下可以做出的选择,例如机器人可以往上,往下,往左,往右走。动作会引起状态的变化
- 奖励:每个动作之后得到的反馈和好处。例如撞墙了,我们给它扣0.5分,没撞墙但是没到终点,我们给它扣0.1分
- 转移概率:在当前状态下执行某个动作后,环境会如何变化,也就是下个状态会是怎样的。例如机器人在行走的过程中,可能因为环境因素滑倒、偏移等,导致机器人执行动作后不能100%的达到预期状态(我们目前的游戏中不考虑这一点)
Q-learning
强化学习中有四个核心概念:策略(Policy)、价值函数(Value Function)、回报(Return)和最优策略(Optimal Policy)
- 策略:决策规则,每个状态下应该做出什么策略
- 价值函数:从某个状态出发,执行一个策略,最终能获得的长期奖励的期望。
- 回报:从某个时刻开始,后续奖励的累计值。
- 折扣回报:在不同的问题中,短期回报和长期回报的重要程度是不同的,所以还需提出折扣回报的概念。如果短期奖励更为重要,则需要对未来奖励做折扣处理,即乘以一个0-1之间的值作为折扣因子使得未来奖励降低
- 最优策略:从任何状态出发,得到的最大累计奖励的策略
强化学习中,Q-learning是一种经典算法,通过学习动作价值函数$Q(s,a)$ 来获得最优策略,其中s为状态state,a为动作action
- 对于每一对状态-动作组合$(s,a)$,Q会维护一个Q值,即期望的回报。
- 初始时,可以把Q值设置成随机数,当然设置成0也可以。
- 每次执行一个动作后,Q值会更新,根据当前奖励和未来状态的Q值来更新
Q值更新公式如下
$Q(s_t,a_t) \leftarrow Q(s_t,a_t)+\alpha [r_t+\gamma \mathop{max}\limits_a Q(s_{t+1},a)-Q(s_t,a_t)]$
公式中$s_t$为当前状态$a_t$为当前动作,$r_t$为当前奖励,$\gamma$为折扣因子,控制未来奖励重要性,$\alpha$为学习率,控制迭代更新速度
当所有的Q值都收敛时,选择每个状态下Q值最大的动作即为最优策略。
机器人走迷宫实现
现在你已经掌握了强化学习的基础,让我们使用python解决机器人走迷宫的问题吧!
首先我们引入必要的库
import numpy as np
import torch
import torch.nn as nn
import torch.optim as optim
import random
import time
import os
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")接着我们定义迷宫环境
# 迷宫环境定义
class MazeEnv:
def __init__(self):
# 统一数据类型: 0空地,1墙,2起点,3终点
self.maze = np.array([
[2, 0, 1, 0, 3],
[1, 0, 1, 0, 1],
[0, 0, 1, 0, 1],
[0, 1, 0, 0, 1],
[0, 0, 0, 1, 1]
])
# 初始化起点和终点位置
self.start_pos = tuple(np.argwhere(self.maze == 2)[0])
self.goal_pos = tuple(np.argwhere(self.maze == 3)[0])
# 重置环境
self.reset()
def reset(self):
# 让智能体(机器人)的位置恢复到起始位置
self.agent_pos = self.start_pos
return self.get_state()
def get_state(self):
# 这个函数的目的是获取一个矩阵表示当前状态。我们定义矩阵中墙的位置为-1,智能体位置为1,目标位置为0.5
state = np.zeros_like(self.maze, dtype=np.float32)
state[self.maze == 1] = -1
state[self.agent_pos] = 1
state[self.goal_pos] = 0.5
# 将矩阵flatten,作为状态向量
return state.flatten()
def step(self, action):
# 有四种行动方向,分别是左、右、上、下
moves = [(-1,0), (1,0), (0,-1), (0,1)]
new_pos = (self.agent_pos[0] + moves[action][0],
self.agent_pos[1] + moves[action][1])
# 默认给一个-0.1的惩罚。防止机器人"不思进取"来回踱步
reward = -0.1
done = False
# 判定机器人是否越界
if (0 <= new_pos[0] < 5 and 0 <= new_pos[1] < 5):
if self.maze[new_pos] != 1:
self.agent_pos = new_pos # 只有非墙才移动
else:
reward = -0.5 # 撞墙给予更严厉惩罚
else:
reward = -0.8 # 越界也惩罚更大
# 如果到达终点,给一个大大滴奖励
if self.agent_pos == self.goal_pos:
reward = 1
done = True
return self.get_state(), reward, done
def render(self):
# 在控制台打印机器人当前的状态
os.system('cls' if os.name == 'nt' else 'clear')
maze_copy = np.array(self.maze, dtype=object)
maze_copy[maze_copy == 0] = ' '
maze_copy[maze_copy == 1] = '█'
maze_copy[maze_copy == 2] = 'S'
maze_copy[maze_copy == 3] = 'G'
maze_copy[self.agent_pos] = 'A'
print("\n".join(["".join(row) for row in maze_copy]))
time.sleep(0.3)接着我们定义DQN网络
class DQN(nn.Module):
def __init__(self, state_size, action_size):
super(DQN, self).__init__()
self.layers = nn.Sequential(
nn.Linear(state_size, 64),
nn.ReLU(),
nn.Linear(64, 64),
nn.ReLU(),
nn.Linear(64, action_size)
)
def forward(self, x):
return self.layers(x)这里我们定义了一个DQN网络,输入状态向量,通过隐藏层,输出决策行为
接着我们写DQN的训练函数
def train():
# 初始化一个迷宫实例
env = MazeEnv()
# 状态空间和动作空间的大小
state_size = env.get_state().shape[0]
action_size = 4
# 初始化一个DQN实例
dqn = DQN(state_size, action_size).to(device)
# 定义Adam优化器,学习率为0.001
optimizer = optim.Adam(dqn.parameters(), lr=0.001)
# 损失函数为MSE
criterion = nn.MSELoss()
# 参数
epsilon = 1.0 # 初始探索概率
epsilon_decay = 0.995 # 探索概率的衰减率
epsilon_min = 0.01 # 探索概率最小值
gamma = 0.9 # 折扣因子
episodes = 300 # 游戏次数
memory = [] # 经验数据
# 开始循环玩游戏
for episode in range(episodes):
# 每次游戏前还原到初始状态
state = env.reset()
done = False
step = 0
# 防止重复循环,最多允许走50步
while not done and step < 50:
step += 1
# 有epsilon的概率随机探索,有1-epsilon的概率根据模型返回的策略探索
if random.random() < epsilon:
action = random.randint(0, action_size - 1)
else:
with torch.no_grad():
q_values = dqn(torch.tensor(state).to(device))
action = torch.argmax(q_values).item()
# 执行动作,获得新状态
next_state, reward, done = env.step(action)
# 存储经验到记忆池
memory.append((state, action, reward, next_state, done))
state = next_state
# 及时剔除老旧的经验
if len(memory) > 1000:
memory.pop(0)
# 从经验池抽选32个经验,优化模型
if len(memory) >= 32:
batch = random.sample(memory, 32)
states, actions, rewards, next_states, dones = zip(*batch)
states = torch.tensor(states).to(device)
actions = torch.tensor(actions).unsqueeze(1).to(device)
rewards = torch.tensor(rewards).to(device)
next_states = torch.tensor(next_states).to(device)
dones = torch.tensor(dones, dtype=torch.float32).to(device)
q_values = dqn(states).gather(1, actions).squeeze()
next_q_values = dqn(next_states).max(1)[0]
targets = rewards + gamma * next_q_values * (1 - dones)
loss = criterion(q_values, targets.detach())
optimizer.zero_grad()
loss.backward()
optimizer.step()
epsilon = max(epsilon_min, epsilon * epsilon_decay)
if episode % 50 == 0:
print(f'Episode: {episode}, Epsilon: {epsilon:.2f}')
torch.save(dqn.state_dict(), 'dqn_maze.pth')
print(dqn.state_dict())
print('训练完成,模型保存为 dqn_maze.pth')接着让我们的机器人玩迷宫吧!
def play():
env = MazeEnv()
state_size = env.get_state().shape[0]
action_size = 4
dqn = DQN(state_size, action_size)
dqn.load_state_dict(torch.load('dqn_maze.pth'))
dqn.eval()
state = env.reset()
done = False
step = 0
env.render()
while not done and step < 20:
step += 1
with torch.no_grad():
q_values = dqn(torch.tensor(state))
action = torch.argmax(q_values).item()
state, reward, done = env.step(action)
env.render()
print()
if done:
print("成功到达终点!")
else:
print("未能到达终点。")运行结果:


