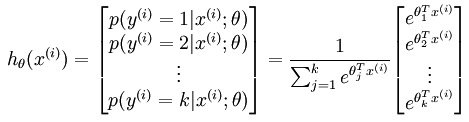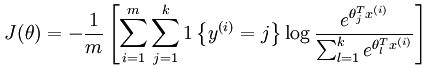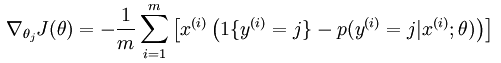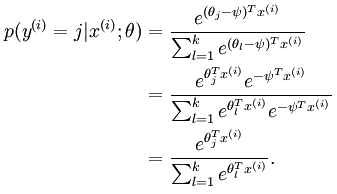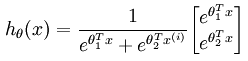前面讲过了Logistic回归,Logistic回归比较简单,实现起来比较容易。
如果现在有一个新的课题:
识别MNIST手写图像(一个大型手写数字0-9的训练集,训练集下载链接:http://yann.lecun.com/exdb/mnist/)
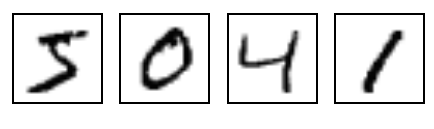
用Logistic如何实现?
很显然Logistic是无法实现的,因为Logistic只能处理二分类问题,而MNIST的输出分类却有10种(0,1,2…..9)。如果强行使用Logistic回归,你可以先判断图片“是0还是非0”,这是的答案只有两种,是或不是,因此这一个二分类问题,可以使用logistic解决。接下来如果非0,继续判断是1还是非1,接着判断是2或非2。但是这样就会十分麻烦。
为了更好的解决多分类这一问题,我们引入了Softmax Regression。
1、Softmax 的假设函数是这样婶儿的:
对于每一项而言,
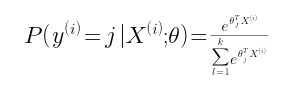
这个函数的意思就是,对于样本Xi,其预测值 yi=j 的概率为后面的式子。θ是参数,分子是计算Xi*θ的指数,分母是将所有yi对应的分子相加,目的是归一化(所有的概率值相加等于1)
用矩阵展开写,就是:
和Logistic回归一样,Softmax回归同样有损失函数:
2、Softmax的损失函数
我们定义一个指示函数:1{x},当x为真的时候,1{x}=1,当x为假的时候,1{x}=0。举两个例子:
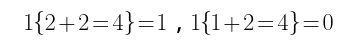
接着是损失函数:
这里面用到了刚刚定义的指示函数1{yi=j},这里的yi=j意思是yi属于第j类。即当且仅当yi属于第j类的时候,1{yi=j}返回1,否则为0。
3、Softmax的梯度下降法:
对Softmax的损失函数求导,得出:
接着使用梯度下降法进行更新参数值:
θj = θj – α*损失函数导数
重复几次就会达到最优值。
4、Softmax参数冗余的特点
什么是参数冗余?简言之,就是参数中有的参数没有作用,造成了多余。我们做一个实验,在参数向量θj中减去向量 φ:
对照前面的假设函数:
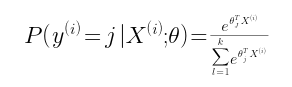
减掉的参数似乎对假设函数没有造成影响诶…..
所以这个模型中,存在多组最优解!
5、Softmax回归与logistic回归的联系
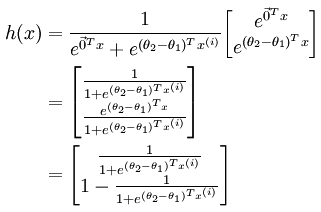
其实logistic回归就是Softmax回归的特殊情况。既然logistic回归只能解决二分类问题,我们就让Softmax回归的类别数量k=2,则Softmax回归算法的假设函数变成:
利用前面说过的,参数冗余的特性,我们将两个参数(θ1和θ2)都减去θ1
令θ‘=θ2-θ1,就会发现,这和logistic回归算法是一毛一样的。