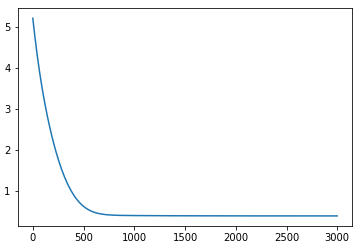
在(二)中,我们的程序实现了前向传播,前向传播是一个预测的过程,在数学角度,是一个矩阵相乘的过程。而反向传播是一个学习的过程,在数学角度就是求导,原理是将输出的数据与真实数据进行对比,从而得到神经网络预测的不足,通过反向传播的“反馈”,计算差值,完善权重参数,得到更加精准的预测结果。
〇、瞎搞点数据
我们想让神经网络学习,又没有合适的数据让他学习,最好的办法就是瞎生成一些特征,然后按照一定的规则通过这些特征生成输出,将这些数据喂给神经网络进行学习。
下面生成的输入X是随机的,对于每个输入X[i],有两个特征X[i][0]和X[i][1],输出Y的规则是:对于每一个输出Y[i],如果X[i]的两个特征之和小于1,则是1,否则是0。
#设置常量,瞎编数据
#每次喂给神经网络几个数据
BATCH_SIZE = 8
#随机种子
seed = 23455
#基于seed产生随机数
rng = np.random.RandomState(seed)
X = rng.rand(32, 2)
Y = [[int(x0 + x1 < 1)] for (x0, x1) in X]
print("X:\n",X)
print("Y:\n",Y)一、搭建模型
这里我们要定义两个占位符,因为在反向传播中,对于每一组输入特征,必须有正确的输出与之对应才能得到反馈。
#占位符,以后存放训练集和对应的标签
x = tf.placeholder(tf.float32, shape=(None, 2))
y_= tf.placeholder(tf.float32, shape=(None, 1))接着初始化权重,这里我们使用正态分布随机数进行初始化:
w1 = tf.Variable(tf.random_normal([2, 3], stddev=1, seed=1))
w2 = tf.Variable(tf.random_normal([3, 1], stddev=1, seed=1))接着计算隐藏层和输出,实现前向传播的过程:
a = tf.matmul(x, w1)
y = tf.matmul(a, w2)为了给神经网络一个反馈,告知它与正确输出的偏离度有多大,我们需要定义一个损失,即loss:
loss = tf.reduce_mean(tf.square(y-y_))这里tf.square表示均方误差。均方误差的表达式:
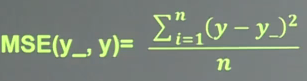
也就是将全部的y-y_的平方求平均。
为了使损失在学习过程中不断减小,我们需要使用优化器。tf中提供了几种常用的优化器,例如:
tf.train.GradientDescentOptimizer(LEARN_RATE).minimize(loss)
tf.train.MomentumOptimizer(LEARN_RATE, MOMENTUM).minimize(loss)
tf.train.AdamOptimizer(LEARN_RATE).minimize(loss)在这里我们先使用梯度下降优化器,以0.001的学习率来减少loss:
train_step = tf.train.GradientDescentOptimizer(0.001).minimize(loss)二、运行模型,迭代优化
#会话
with tf.Session() as sess:
init_op = tf.initialize_all_variables()
sess.run(init_op)
#开始训练
STEPS = 3000 #训练次数
for i in range(STEPS):
start = (i * BATCH_SIZE) % 32
end = start + BATCH_SIZE
sess.run(train_step, feed_dict={x:X[start:end], y_:Y[start:end]})
#每500次计算一次损失
if i % 500 == 0:
total_loss = sess.run(loss, feed_dict = {x:X, y_:Y})
print("Now %d steps, loss:%g" % (i, total_loss))通过matplotlib绘图,loss的变化:
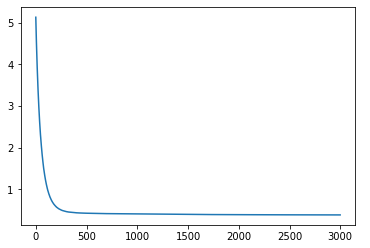
另外两种优化器的loss:
MomentumOptimizer(0.001, 0.9)
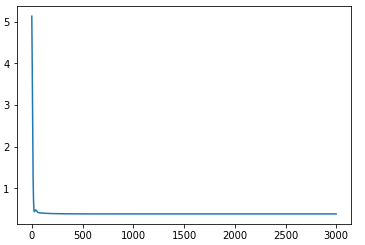
AdamOptimizer(0.001):