0x00、Dijkstra并不是万能的
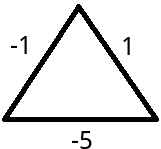
前面我们讲过了Dijkstra算法,Dijkstra算法可以很好的解决边权均为正数的最短路径问题,但是,请看下图:
(上面的点是A,左边的是B,右边的是C,作图的时候忘记打上去了TAT...)
如果我们使用Dijkstra来解决从A走向,我们的思路如下:
-
当前在A点,标记A已访问,设置MinDistance[B]= -1;MinDistance[C] = 1
-
因为MinDistance[B]最小,所以走到B,标记B已访问
-
当前在B,我们使用B去更新没有访问的邻接点,MinDistance[C] = -6
-
全部节点遍历完毕
此时MinDistance[B] = -1,但是我们知道,沿着路线A->C->B走,会得到更短的路线:-4,所以使用Dijkstra解得的答案是错误的
为了解决带有负权的最短路径问题,我们就需要学习Bellman-Ford算法。
0x01、三种不同的环
先引入三种环的定义:
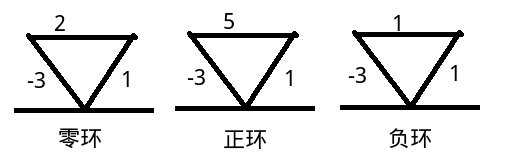
将边权之和不同的环分别称为零环、正环、负环。在这里,零环和正环不会影响到我们最短路径的求解,因为如果是零环,我们走进去和没走进去是一样的,而正环走进去比不走进去的总路径长度还要多。只有负环才会有"走到环里比不走到环里的路径更短",所以我们只讨论负环。
与Dijkstra算法相同,我们准备一个数组MinDistance,存放该点到起点的最短路径。同时Bellman-Ford算法要返回一个bool类型的值,表示是否存在从起点可以到达的负环。
在Bellman-Ford算法中,遍历是从起点到终点按照顺序进行遍历,而不是像Dijkstra那样定义visited数组(判断是否访问过该点)来判断是否应该遍历。
伪代码如下:
for(int i = 0; i < n - 1; i++){ //n为顶点数,进行n-1轮操作
for(每一个从u->v的边){ //每一轮操作都要遍历每一条边
if(d[u] + length[u->v] < d[v]){ //以u为中介点,可以使d[v]更小
d[v] = d[u] + length[u->v]; //更新数组d里面的最短距离
}
}
}此时,如果图中没有从起点可以到达的负环,则数组d中的所有值应该已经达到了最优。接下来我们判断是否存在起点可达的负环
判断是否存在从起点出发可以到达的负环,我们只需对所有变进行一轮遍历,判断是否存在某条边 u->v ,仍然满足d[u] + length[u->v] < d[v]。如果有,就说明图中存在从起点可以到达的负环。
for(每一个从u->v的边){
if(d[u] + length[u->v] < d[v])
return false; //说明图中有源点可达的负环
}
return true; //没有这了Bellman算法的证明就不写了。。有兴趣的同学可以参考《算法笔记》这一节的讲解。。
0x02、C语言实现
由于Bellman-Ford算法需要遍历所有的边,所以使用邻接表会比较方便,代码如下:
struct Node{
int v, dis; //v为邻接边的目标顶点,dis为邻接边的边权
};
vector<Node> Adj[MAXV]; //图的邻接表
int n; //顶点数
int d[MAXN]; //起点到各点的距离(MinDistance)
bool Bellman(int s){ //s为起点
fill(d, d + MAXN, INF); //初始化,INF为一个非常大的数
d[s] = 0; //起点到自身的距离为0
//开始求解数组d
for(int i = 0; i < n - 1; i++){ //执行n-1轮操作,其中n为顶点数
for(int u = 0; u < n; u++){ //每轮操作遍历一遍所有的边
for(int j = 0; j < Adj[u].size(); j++){ //遍历当前边的邻接边
int v = Adj[u][j].v; //v是当前边的邻接边的目标顶点
int dis = Adj[u][j].dis; //dis是当前边的临街边的边权
if(d[u] + dis < d[v]){
d[v] = d[u] + dis; //更新最短路径(松弛操作)
}
}
}
}
//开始判断是否有源点可达的负环
for(int u = 0; u < n; u++){
for(int j = 0; j < Adj[u].size(); j++){
int v = Adj[u][j].v; //邻接边的顶点
int dis = Adj[u][j].dis; //邻接边的边权
if(d[u] + dis < d[v])
return false;
}
}
return true;
}