原题干:
An AVL tree is a self-balancing binary search tree. In an AVL tree, the heights of the two child subtrees of any node differ by at most one; if at any time they differ by more than one, rebalancing is done to restore this property. Figures 1-4 illustrate the rotation rules.
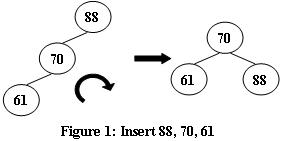
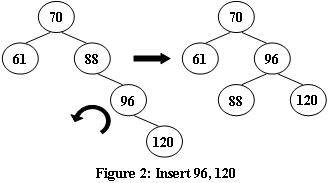
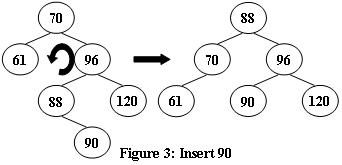
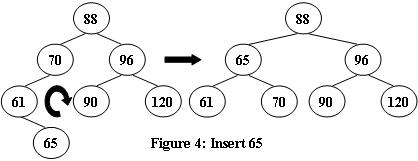
Now given a sequence of insertions, you are supposed to tell the root of the resulting AVL tree.
Input Specification:
Each input file contains one test case. For each case, the first line contains a positive integer N (<=20) which is the total number of keys to be inserted. Then N distinct integer keys are given in the next line. All the numbers in a line are separated by a space.
Output Specification:
For each test case, print ythe root of the resulting AVL tree in one line.
Sample Input 1:
5 88 70 61 96 120
Sample Output 1:
70
Sample Input 2:
7 88 70 61 96 120 90 65
Sample Output 2:
88
题目的意思很简单,给定一串序列,插入到AVL树中,要求给定插入后根节点的数值
因为发生了旋转,所以根节点的数值不一定是第一个数...
其实这道题只输出中位数就会得很多分。。。
根据这篇文章可以理解这道题的主要操作:平衡二叉树(AVL树)的基本操作 - 斐斐のBlog
代码如下:
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
/**
* 二叉树结构体
*/
struct node{
int data, height;
node *lchild, *rchild;
} *tree;
/**
* 获取节点高度方法
* 参数:节点指针
* 返回:int,高度值
*/
int GetHeight(node* root){
return root == NULL ? 0 : root->height;
}
/**
* 计算平衡因子方法
* 参数:节点指针
* 返回:int,平衡因子
*/
int GetBalance(node* root){
return root == NULL ? 0 : (GetHeight(root->lchild) - GetHeight(root->rchild));
}
/**
* 更新节点高度方法
* 参数:要更新的节点指针
*/
void updateHeight(node* root){
root->height = max(GetHeight(root->lchild), GetHeight(root->rchild)) + 1;
return;
}
/**
* AVL树的LL型旋转
* 单次右旋
* 参数:根节点
*/
void LL(node* &root){
node *temp = root->lchild;
root->lchild = temp->rchild;
temp->rchild = root;
updateHeight(root);
updateHeight(temp);
root = temp;
}
/**
* AVL树的RR型旋转
* 单次左旋
* 参数:根节点
*/
void RR(node* &root){
node *temp = root->rchild;
root->rchild = temp->lchild;
temp->lchild = root;
updateHeight(root);
updateHeight(temp);
root = temp;
}
/**
* AVL树的LR型旋转
* 参数:根节点
*/
void LR(node* &root){
RR(root->lchild);
LL(root);
}
/**
* AVL树的RL型旋转
* 参数:根节点
*/
void RL(node* &root){
LL(root->rchild);
RR(root);
}
/**
* AVL树递归插入方法
* 参数:根节点,要插入的数据
*/
void insert(node* &root, int data){
if(!root){ //插入点
root = new node;
root->data = data;
root->lchild = root->rchild = NULL;
root->height = 1;
return;
}else{ //非插入点
if(root->data > data){ //根节点数据大,应该往左插
insert(root->lchild, data);
updateHeight(root);
if(GetBalance(root) == 2 && GetBalance(root->lchild) == 1)
LL(root);//LL型,单次右旋
else if(GetBalance(root) == 2 && GetBalance(root->lchild) == -1)
LR(root);//LR型,先左后右
}else{ //根节点小或等,往右插
insert(root->rchild, data);
updateHeight(root);
if(GetBalance(root) == -2 && GetBalance(root->rchild) == 1)
RL(root);//RL型,先右后左
else if(GetBalance(root) == -2 && GetBalance(root->rchild) == -1)
RR(root);//RR型,单次左旋
}
}
}
int main(){
int cnt, tmp;
cin >> cnt;
while(cnt--){
cin >> tmp;
insert(tree, tmp);
}
cout << tree->data << endl;
return 0;
}
