0x00、树(Tree)
树是一种和链表一样重要的数据结构,与链表不同的是,树有着层次结构。
现实生活中的树,是由树根(root),树枝(edge),节点叶子(leaf)组成的。
在数据结构中的树,就像是把数连根拔起,再四单脚朝天,也就是把现实生活中的树倒了过来。
树根位于顶部,树根向下形成了若干个树枝,树枝又向下形成了更多的树枝,向下延伸到达子节点(child),形成子树(subtree)
0x01、树的基本定义
下面是几个关于数的定义:
1,树可以没有节点,称之为空树(empty tree)
2,树是有层级(layer)之分的,根节点为第一层,根节点的子节点为第二层,根节点的子节点的子节点为第三层。以此类推
3,把节点的子树的棵树称为节点的度(degree),树中节点最大的度称为数的度,或树的宽度。上面图片的度为3
4,有n个节点的树(根节点也算一个节点)一定有(n-1)条边
5,叶子被定义为 度为0的节点,树中只有一个根节点的时候,根节点也算叶子
6,结点的深度(depth)指从根节点(根节点深度为1)开始,自顶向下逐层累加至该节点的深度值。结点的高度(height)指从最底层叶子结点(高度为1)开始,自底向上逐层累加至该节点的高度值。树的深度指的是树中结点的最大深度。树的高度是指树中结点的最大高度。一般来说,树的深度和高度是相等的。上面图片中的树的高度和深度都是3
7,多棵树组合在一起,称之为森林(forest)
0x02、二叉树的递归定义
二叉树是一种很重要的树,下面是它的定义:
1,如果二叉树没有根节点,则二叉树是一棵空树。
2,如果二叉树有结点,则二叉树由根节点、左子树、右子树构成。而且左子树和右子树都是二叉树。
二叉树的递归定义是一个很好理解的定义:
我们把二叉树想象称为亲缘血统关系,在血缘关系中,爷爷可以用“爸爸的爸爸”来表示,曾祖父可以用“爸爸的爸爸的爸爸”来表示。所以整个家谱都可以用“爸爸”来表示,这样就叫做递归定义。
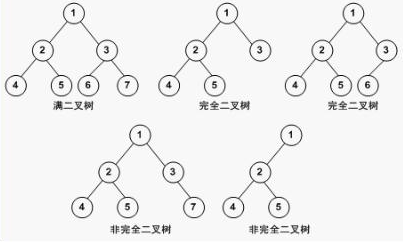
下面是两种特殊的二叉树:
1,二叉树每一层节点个数都达到了当层所能达到的最大节点数,称之为满二叉树
2,二叉树除了最下面的一层,其余节点都达到了当层所能达到的最大节点数,称之为完全二叉树
如上图所示。
0x03、二叉树的C语言实现
二叉树的定义类似链表,与链表不同的是,链表只有一个指向下一节点的指针,而二叉树有两个分别指向左节点与右节点的指针。
定义方式如下:
struct node{
ElementType data;
node* lchild; //LeftChild
node* rchild; //RightChild
};这样我们定义了二叉树的结构,下面我们定义一棵空树:
node* root = NULL;接着创建节点:
node* newNode(int v){
node* Node = new node; //申请node类型的地址空间
Node->data = v; //写入数据
Node->lchild = Node->rchild = NULL; //节点初始状态没有左右child
return Node;
}我们可以使用递归来搜索二叉树中的数据:
void search(node* root, int x){
if(root == NULL)
return;
if(root->data == x)
//找到了
;
search(root->lchild, x); //本节点没有,继续递归查找左节点
search(root->rchild, x); //左节点也没有,查找右节点
}这段代码和DFS算法比较相似。具体问题要根据情况具体分析。在后面的文章中会详细讲解二叉树的遍历。