0x00、仍然从迷宫说起
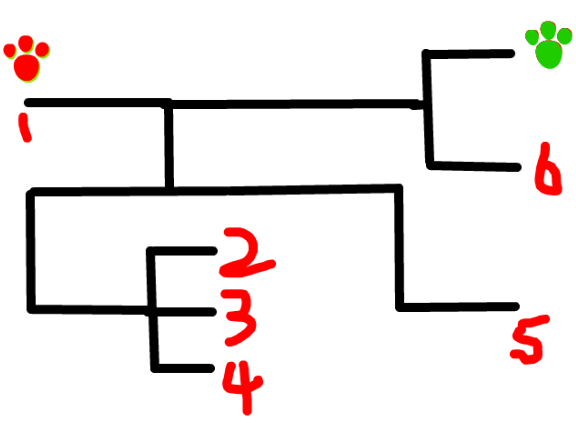
昨天的文章(深度优先搜索),使用迷宫介绍了深度优先搜索,在介绍广度优先搜索前仍然以这个迷宫来介绍。
在深度优先搜索中,我们使用了朝向一个方向,全部遍历的方法,遍历了迷宫,走到了终点,在广度优先搜索中我们采取的措施有些不同:
用图来表示:
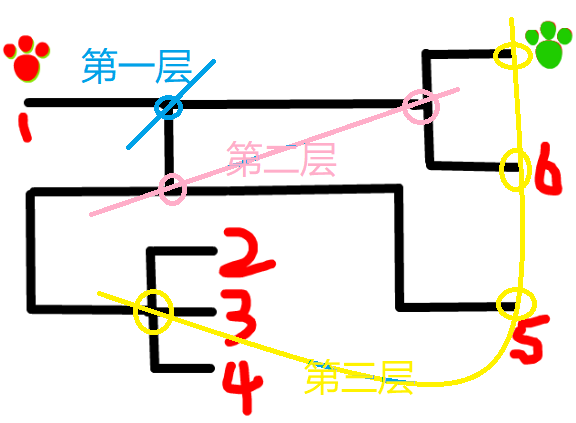
我们使用了层级,遍历迷宫
如果没有看不懂没关系,下面详细的讲解。
0x01、广度优先搜索的实现方式
我们使用一个队列来遍历迷宫:
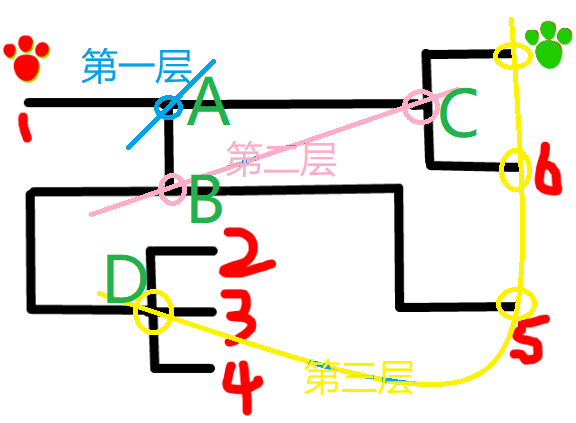
我们先给岔路口编号,A,B,C和D,然后我们新建一个队列,放入第一层的节点,也就是{A}
下面,我们遍历队首元素A,首先让A出队,A的子节点有B和C,我们让B和C入队,队列状态为{B, C}
接着我们遍历队首元素B,B出队,B的子节点为D和5,入队。队列状态为{C, D, 5}
下面继续遍历队首元素C,C出队,C的子节点有终点和6,入队。队列状态为{D, 5, 终点, 6}
继续遍历队首的D,D出队,D的子节点2,3,4入队,队列状态为{5, 终点, 6, 2, 3, 4}
遍历队首元素5,5出队,发现5是死胡同了,停止。队列状态为{终点, 6, 2, 3, 4}
遍历队首元素"终点",发现是终点,停止BFS函数的执行,得出结果。
这种遍历的方式,我们称之为广度优先搜索,简称BFS(Breadth First Search)。
0x02、使用C语言实现广度优先搜索
广度优先搜索使用队列实现,基本写法如下:
void BFS(int s){
queue<int> q;
q.push(s);
while(!q.empty()){
取队首;
访问队首;
弹出队首;
队首元素下一层级的元素全部入队;
}
}这里使用while循环实现,只要队列仍然有元素,就会不断遍历,直到找到终点。
0x03、举个例子
给出一个m*n的矩阵,矩阵的元素为0或1,定义 "相邻" 为上下左右四个位置。如果矩阵中有若干个 1 是相邻的(不必两两相邻),则这些 1 构成了一个"块",求给定矩阵中"块"的个数。单个 1 也算一块。
例如:
0 1 1 1 0 0 1 左边的6*7矩阵中
0 0 1 0 0 0 0 "块"的个数为4
0 0 0 0 1 0 0
0 0 0 1 1 1 0
1 1 1 0 1 0 0
1 1 1 1 0 0 0
在pat乙级中刷过这样类似的图案问题,我们可以定义一个表示"偏移量"的数组
int X[] = {0, 0, 1, -1};
int Y[] = {1, -1, 0, 0};这样,(X[1],Y[1]),(X[2],Y[2]),(X[3],Y[3]),(X[4],Y[4])就是四组偏移量。表示四个方向。
这个偏移量使用的时候可以使用for循环来枚举方向,确定坐标。
for(int i = 0; i < 4; i++){
newX = nowX + X[i];
newY = nowY + Y[i];
}接着我们定义矩阵。矩阵的每个点应当存储输入的数值(data),并存储是否处理过该点(flag)。我们使用结构定义数组。
int n, m; //矩阵大小为n*m
typedef struct{
int data;
bool flag;
} point;
point matrix[100][100];为了方便,我们使用结构体定义坐标,并定义一个坐标类型的全局变量:Node
typedef struct{
int x, y;
} node;
node Node;我们可以使用一个裁定函数(judge)判断这个点是否应该入队。这个函数我们稍后实现。
我们先来实现BSF广度优先搜索函数。
void BFS(int x, int y){
queue<node> Q; //定义队列
Node.x = x, Node.y = y; //当前点的坐标
Q.push(Node); //将该点压入队列
matrix[x][y].flag = true; //将该点标记设置为 已入队
while(!Q.empty()){
node top = Q.front(); //取出队首
Q.pop(); //队首出队
for(int i = 0; i < 4; i++){ //循环4次,遍历四个方向
int newX = top.x + X[i];
int newY = top.y + Y[i]; //newX和newY在这四次循环中分别是4个方向上的点
if(judge(newX, newY)){ //如果这个点需要访问
Node.x = newX, Node.y = newY; //让下一步处理的点变成这个需要等待处理的点
Q.push(Node); //将这个点压入队列,在队尾等待处理。
matrix[newX][newY].flag = true; //标记这个点已经入队。以后无需判断了
}
}
}
}这里面用到了judge函数,这个函数要求:
1,已入队的、曾经判断过的(flag=true)无需再次判断
2,该点为0的,肯定不是一个块的某个元素,无需判断
3,超过矩阵边界,会造成数组溢出,直接返回false,不可以判断
根据这三点,我们轻松的写出了judge函数
bool judge(int x, int y){
/*数组越界情况*/
if(x >= n || x < 0 || y >= m || y < 0)
return false;
/*当前位置为0,一定不是块元素,无需判断*/
if(!matrix[x][y].data)
return false;
/*当前位置已经判断过了,或者已入队,无需重复判断*/
if(matrix[x][y].flag)
return false;
/*以上都不满足,说明是一个从未判断过,并且数值为1的点,返回真*/
return true;
}OK,上面我们完成了广度优先搜索算法的全部步骤。下面我们来完成主函数:
int main(){
cin >> n >> m; //输入矩阵大小
for(int x = 0; x < n; x++)
for(int y = 0; y < m; y++){
cin >> matrix[x][y].data;
matrix[x][y].flag = false;
}
int result = 0; //块数
for(int x = 0; x < n; x++){
for(int y = 0; y < m; y++){
if(matrix[x][y].flag == false && matrix[x][y].data == 1){
result++;
BFS(x, y);
}
}
}
cout << "块数为:" << result << endl;
return 0;
}完整全部代码:
#include <iostream>
#include <queue>
using namespace std;
/*定义矩阵*/
int m, n;
typedef struct{
int data;
bool flag;
} point;
point matrix[100][100];
typedef struct{
int x, y;
} node;
node Node;
/*偏移量相关*/
int X[] = {0, 0, 1, -1};
int Y[] = {1, -1, 0, 0};
bool judge(int x, int y){
/*数组越界情况*/
if(x >= n || x < 0 || y >= m || y < 0)
return false;
/*当前位置为0,一定不是块元素,无需判断*/
if(!matrix[x][y].data)
return false;
/*当前位置已经判断过了,或者已入队,无需重复判断*/
if(matrix[x][y].flag)
return false;
/*以上都不满足,说明是一个从未判断过,并且数值为1的点,返回真*/
return true;
}
/*广度优先搜索函数*/
void BFS(int x, int y){
queue<node> Q; //定义队列
Node.x = x, Node.y = y; //当前点的坐标
Q.push(Node); //将该点压入队列
matrix[x][y].flag = true; //将该点标记设置为 已入队
while(!Q.empty()){
node top = Q.front(); //取出队首
Q.pop(); //队首出队
for(int i = 0; i < 4; i++){ //循环4次,遍历四个方向
int newX = top.x + X[i];
int newY = top.y + Y[i]; //newX和newY在这四次循环中分别是4个方向上的点
if(judge(newX, newY)){ //如果这个点需要访问
Node.x = newX, Node.y = newY; //让下一步处理的点变成这个需要等待处理的点
Q.push(Node); //将这个点压入队列,在队尾等待处理。
matrix[newX][newY].flag = true; //标记这个点已经入队。以后无需判断了
}
}
}
}
int main(){
cin >> n >> m; //输入矩阵大小
for(int x = 0; x < n; x++)
for(int y = 0; y < m; y++){
cin >> matrix[x][y].data;
matrix[x][y].flag = false;
}
int result = 0; //块数
for(int x = 0; x < n; x++){
for(int y = 0; y < m; y++){
if(matrix[x][y].flag == false && matrix[x][y].data == 1){
result++;
BFS(x, y);
}
}
}
cout << "块数为:" << result << endl;
return 0;
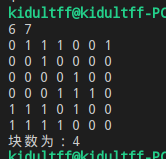
}运行结果: