原题干:
Given a non-empty tree with root R, and with weight Wi assigned to each tree node Ti. The weight of a path from R to L is defined to be the sum of the weights of all the nodes along the path from R to any leaf node L.
Now given any weighted tree, you are supposed to find all the paths with their weights equal to a given number. For example, let's consider the tree showed in Figure 1: for each node, the upper number is the node ID which is a two-digit number, and the lower number is the weight of that node. Suppose that the given number is 24, then there exists 4 different paths which have the same given weight: {10 5 2 7}, {10 4 10}, {10 3 3 6 2} and {10 3 3 6 2}, which correspond to the red edges in Figure 1.
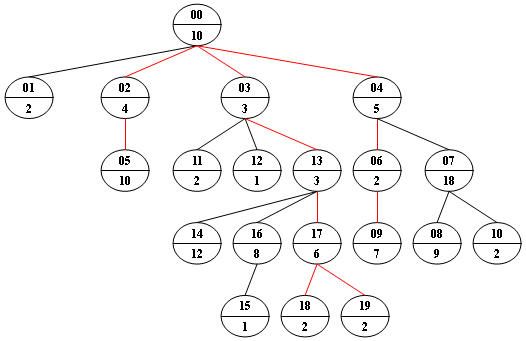
Figure 1
Input Specification:
Each input file contains one test case. Each case starts with a line containing 0 < N <= 100, the number of nodes in a tree, M (< N), the number of non-leaf nodes, and 0 < S < 230, the given weight number. The next line contains N positive numbers where Wi (<1000) corresponds to the tree node Ti. Then M lines follow, each in the format:
ID K ID[1] ID[2] ... ID[K]
where ID is a two-digit number representing a given non-leaf node, K is the number of its children, followed by a sequence of two-digit ID's of its children. For the sake of simplicity, let us fix the root ID to be 00.
Output Specification:
For each test case, print all the paths with weight S in non-increasing order. Each path occupies a line with printed weights from the root to the leaf in order. All the numbers must be separated by a space with no extra space at the end of the line.
Note: sequence {A1, A2, ..., An} is said to be greater than sequence {B1, B2, ..., Bm} if there exists 1 <= k < min{n, m} such that Ai = Bi for i=1, ... k, and Ak+1 > Bk+1.
Sample Input:
20 9 24 10 2 4 3 5 10 2 18 9 7 2 2 1 3 12 1 8 6 2 2 00 4 01 02 03 04 02 1 05 04 2 06 07 03 3 11 12 13 06 1 09 07 2 08 10 16 1 15 13 3 14 16 17 17 2 18 19
Sample Output:
10 5 2 7 10 4 10 10 3 3 6 2 10 3 3 6 2
生词:
greater than:大于 For the sake of simplicity:为了简化
大意:
第一行给出树的总节点数、非叶子节点个数、和一个常数S
接着按照节点编号0,1,2...的顺序,给出所有节点的权重(数据域)
第三行开始,给出所有非叶子节点的子节点(当然叶子节点不存在子节点)
给出的格式为节点"编号 子节点个数 节点地址 节点地址 ...
按照路径最大的原则输出途径数据域
这道题可以由于给定了节点编号的关系,所以我们使用静态二叉树来做。
使用深度优先搜索遍历树,并求解。
在排序上,可以对每个非叶子节点的孩子域进行排序,按照孩子域从大到小进行排序。
代码如下:(使用旧版本的编译器可能编译不通过,请使用最新版的gcc编译器)
#include <iostream>
#include <algorithm>
#include <vector>
#include <cstdio>
using namespace std;
vector<int> T[101]; //静态树
int T_V[101] = {0}; //点权
int all_cnt, no_leaf_cnt, weight;
vector<vector<int> > Path; //存放路径的容器
vector<int> tmpPath; //存放临时路径的容器
void DFS(int s, int w){
tmpPath.push_back(T_V[s]);
w += T_V[s];
if(T[s].size() == 0){ //递归边界
if(w == weight) //这条路径可以欸
Path.push_back(tmpPath);
}else{ //递归式
for(int i = 0; i < T[s].size(); i++)
DFS(T[s][i], w);
}
tmpPath.pop_back();
w -= T_V[s];
}
bool cmp(vector<int> &a, vector<int> &b){
for(int i = 0;
i < a.size() && i < b.size();
i++){
if(a[i] != b[i]) return a > b;
}
return a.size() > b.size();
}
int main(){
cin >> all_cnt >> no_leaf_cnt >> weight;
for(int i = 0; i < all_cnt; i++)
cin >> T_V[i]; //读入静态树点权
for(int i = 0; i < no_leaf_cnt; i++){
int n, cnt;
cin >> n >> cnt;
for(int j = 0; j < cnt; j++){
int _;
cin >> _; //读入静态树孩子
T[n].push_back(_);
}
}
DFS(0, 0);
sort(Path.begin(), Path.end(), cmp);
for(auto it : Path){
for(int i = 0; i < it.size(); i++){
if(i) cout << ' ';
cout << it[i];
}
cout << endl;
}
return 0;
}
