0x00、堆
堆是一种特殊的完全二叉树,堆分为大顶堆和小顶堆,其中大顶堆是指二叉树的任何一个非叶子结点都比其孩子大,小顶堆则反之。
假设给定一个序列:

其对应的大顶堆就可以是:
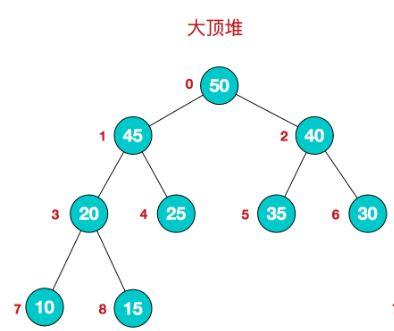
小顶堆就是:
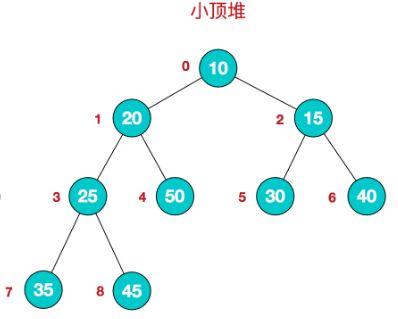
那么这个程序怎样用C语言来实现呢?
0x01、建堆
我们使用数组,即静态二叉树来保存堆,定义的时候一般情况下不选用下标为0的位置来存储数据,下标为0的位置通常使用一个很大的数字或者很小的数字作为哨兵变量。
我们在全局变量中定义堆:
int heap[] = {-1, 20, 35, 25, 30, 45, 10, 40, 50, 15}; //-1为哨兵变量
int n = 9; //堆中元素个数对于这个堆的i个节点而言,下标为2i的位置是它的左孩子,下标为2i+1的位置是它的右孩子。
如果想要建成大顶堆,我们就需要保证每个非叶子节点都比其左右孩子大,根节点与叶子节点比较调整,我们称之为向下调整
向下调整的代码实现:
void DownAdjust(int low, int high){
int i = low, j = i * 2; //i存放要调整的节点,j存放其左孩子
while(j <= high){ //j没越界,说明存在孩子节点
if(j+1 <= high){ //防止不存在右孩子而导致越界
if(heap[j + 1] > heap[j]) //右孩子更大
j= j + 1; //让j存放右孩子的下标
}
//如果孩子中最大的值比欲调整节点i大
if(heap[j] > heap[i]){
swap(heap[j], heap[i]);//交换最大的孩子与要调整的节点i
i = j; //保持i为要调整的节点
j = i * 2; //j为i的左孩子
}else
break; //孩子都比要调整的i小,调整结束
}
}这样,就实现了对一个节点的调整。
向下调整还有一种递归写法,递归终点是无孩子节点或者堆的顺序已经正确:
void DownAdjust(int low, int high){
int i = low, j = i * 2; //i是要调整的节点,j是左孩子
if(j > high) return; //如果没有左孩子(越界),直接返回
int max_index = heap[i] > heap[j] ? i : j; //在左孩子与要调整的节点中找到最大的下标
//如果存在右孩子,在刚刚找到的最大的下标和右孩子中找最大的
if(j + 1 < high) max_index = heap[max_index] > heap[j + 1] ? max_index : (j + 1);
if(max_index == i) return; //如果要调整的节点已经是最大的了,顺序正确,直接返回
swap(heap[i], heap[max_index]); //执行交换
DownAdjust(max_index, high); //递归调整
}为了方便操作,我们从最后一个非叶子节点进行调整。
最后一个非叶子节点的位置是n/2。
我们只需要从最后一个非叶子节点的位置向前遍历一遍即可。
void CreateHeap(){
for(int i = n / 2; i >= 1; i--)
DownAdjust(i, n);
}调用这个函数,运行结果为:
int main(){
CreateHeap();
for(int i = 0; i <= n; i++)
cout << heap[i] << ' ';
return 0;
}
0x02、删除顶部元素
删除顶部元素,我们只需要用最后一个元素覆盖掉顶部的元素,并让堆元素个数减去1,再进行调整即可:
void DeleteTop(){
heap[1] = heap[n--];
DownAdjust(1, n);
}执行结果:
int main(){
CreateHeap();
DeleteTop();
for(int i = 0; i <= n; i++)
cout << heap[i] << ' ';
return 0;
}
可以看到,堆顶元素已经被删除了
0x03、插入元素
往堆中插入元素,可以先将元素插入到堆的末尾,然后执行一次向上调整。
向上调整和向下调整正好相反,是由每个叶子节点与根节点进行比较:
void UpAdjust(int low, int high){
int i = high, j = i / 2; //i是要调整的节点,j是i的父亲
while(j >= low){ //越界说明父亲节点不存在
if(heap[j] < heap[i]){ //如果父亲比叶子小
swap(heap[j], heap[i]); //交换
i = j; //保持i是要调整的节点
j = i / 2; //j是i的父亲
}else break; //父亲比i大,调整结束
}
}同样的,向上调整也有一种递归写法
void UpAdjust(int low, int high){
int i = high, j = i / 2; //i为要调整的节点,j为父亲节点
if(j < low) return; //越界,到达递归终点,直接返回
if(heap[i] > heap[j]){ //如果父亲节点比要调整的节点小
swap(heap[i], heap[j]); //执行交换
UpAdjust(low, j); //递归调整
}
}插入元素:
void Insert(int x){
heap[++n] = x;
UpAdjust(1, n);
}测试一下这个函数:
int main(){
CreateHeap();
DeleteTop();
Insert(32);
for(int i = 0; i <= n; i++)
cout << heap[i] << ' ';
return 0;
}执行结果:

0x04、堆排序
这里以大顶堆为例,对于一个大顶堆而言,顶端元素永远是最大的,因此我们可以不断地抽出顶端元素,再向下调整,抽出顶端元素,再调整,这样就可以得到一个有序的序列了。
void HeapSort(){
CreateHeap(); //排序前先建堆
for(int i = n; i > 1; i--){ //最大的元素移动到了数组的末尾,这些有序序列不参加调整
swap(heap[i], heap[1]); //将堆中最后一个元素与堆顶元素交换,从而将堆顶加入到末尾有序序列中,交换后相当于删除了堆顶
DownAdjust(1, i - 1); //向下调整,保证堆顶是剩下元素中最大的
}
}测试一下:
int main(){
HeapSort();
for(int i = 0; i <= n; i++)
cout << heap[i] << ' ';
return 0;
}运行结果:



博主您好,文章写的很好。DownAdjust的递归方法if(j + 1 < high)应该为if(j + 1 <= high),你再确认下呢