0x00、基本概念及相关术语
什么是图?图就是类似地图的一种东西,类似这种:
(博主家乡高清无♂码的交通路线图)
从图中可以看出,一张图由顶点(Vertex)、边(Edge),两部分组成。每条边的两端都一定是图的顶点。
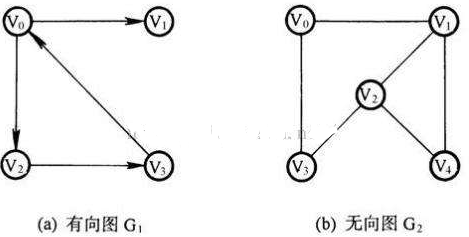
图可以分为两种:有向图和无向图。像这样:
顾名思义,前者就是有方向的意思,后者无方向。
图还有几个重要的概念:
某顶点的"度"是指和该顶点项链的边的条数。对于有向图来说,顶点的出度指的是顶点的出边条数(从顶点指向外侧)。反过来,入边条数就称为入度。
顶点和边都有一定的属性,量化的属性称为权值。顶点的权值称为点权,边的权值称为边权。
其实这些定义很好理解。比如对于上面的高清无♂码呼伦贝尔交通图,点,就是城市数量。边,就是路径条数;某个城市的度,就是连接某个城市的道路的条数。
点权可以认为是城市中资源的数目;边权可以认为是两个城市之间路途上的消费。
0x02、图的存储
一般来说,图的存储方式有两种:邻接矩阵和邻接表。两种存储方式各有优势,根据实际情况选择使用。
1、邻接矩阵
邻接矩阵是一种非常简单的存储图的方式,例如一个图的顶点编号分别为0,1,2,前面说过,图中的一条边是要连接两个点的,所以我们可以用坐标的形式来表示边。例如(1,2),表示 1 和 2 之间连着的边。
我们开一个二维数组,记做G,则 G[N][M]可以表示"N与M之间的边"。
这样,我们就可以使用一个矩阵来表示整张图了。在边存在的地方,令对应的邻接矩阵的值为1,不存在的地方令邻接矩阵的值为0即可。这样的矩阵就叫做邻接矩阵。
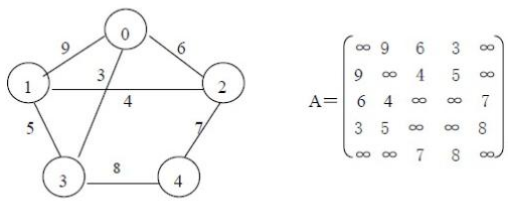
比如下面这张图就是个邻接矩阵↓↓↓↓↓↓↓
这个图有4个点、4个边;邻接矩阵为A。V0和V1之间存在边,所以A[0][1] = 1;而V3和V2之间不存在边,所以A[3][2] = 0
而如果我们要记录边权信息,我们就不能单独的记录0和1了。将 边 对应的 邻接数组的值 设置为 边权值,将 边权不存在的地方 对应的 邻接数组的值 设置为0,或者-1,或者非常大的数字。这样就可以记录下边权信息了。
比如这样↓↓↓↓↓↓↓
由于0和1之间存在边,且边权为9,所以A[0][1] = 9;而0和4之间不存在边,更不存在边权,所以A[0][4] = ∞
如果要记录点权的信息,一般的做法是开一个一维数组记录。
上面就是邻接矩阵的全部内容。同时我们可以观察到,无向图的邻接矩阵一定是绕着对角线对称的。
邻接矩阵比较容易写,但是由于数组的利用率比较低,所以大大浪费了内存空间。邻接矩阵比较适合顶点数目不太大的题目。如果顶点过多,一般使用邻接表的方式来存储。
2、邻接表
数组的特征是容易写,但是空间利用率不高,大型数组占用内存过大。链表可以很好的解决这一问题。于是邻接表的图存储方式应运而生。
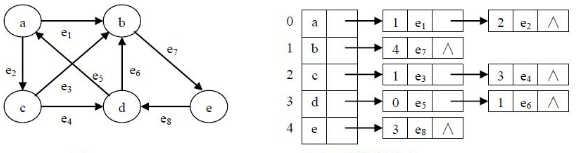
假设图的顶点为1,2,3...N,则这N个顶点中,每个顶点都可能有若干条出边。如果把同一个顶点的 所有出边 都放在一个列表中,那么N个顶点就有N个列表。如果没有出边,则另其对应的列表为空表。这N个列表就称为邻接表。
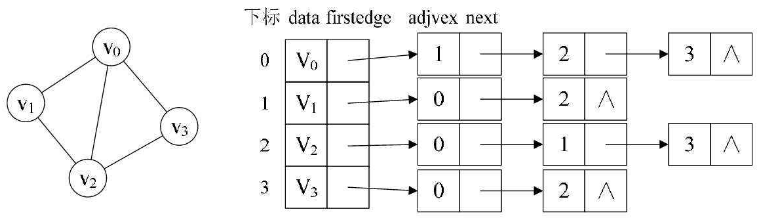
下面这张图就是一个邻接表↓↓↓↓↓↓↓
因为V0有三条出边:V1、V2、V3,所以V0对应的链表结构为V0->V1->V2->V3->NULL
如果边权存在,我们可以在链表的每个节点开一个存储边权的地方。像这样↓↓↓↓↓↓↓
对于链表,这里不推荐直接用真正的链表来完成,用vector会简单的很多,下面来一起用vector写一个邻接表:
首先定义一个数组,存储邻接表。数组的每个单元都是列表(vector)。
vector<int> adj[N];这样adj数组就是一个邻接表,比如点 1 有一条出边终点为 3 ,可以用这样的代码来实现:
adj[1].push_back(3);上面的邻接表是无权的。对于有边权的邻接表,我们只要在邻接表的每个单元加入记录边权的变量即可。用struct来实现:
typedef struct{
int v; //边的终点编号
int w; //边权
} node;
vector<node> adj[N];这样就加上了边权信息。例如点 1 有一条出边终点 3 ,边权为 4 ,可以这么写
node tmp; //临时变量
tmp.v = 3; //出边终点为3
tmp.w = 4; //边权为4
adj[1].push_back(tmp); //将定义好的临时变量放入容器