C++实现二阶Runge-Kutta算法

算法描述详见《微分方程数值解》或《数值分析》

直接上代码：

/**
* Runge-Kutta Algorithm
* @author Kidultff
* @Time 2019-03-15 15:15
*/
#include <bits/stdc++.h>
using namespace std;
/**
* 待求解的微分方程
* @param x与y的值
* @return y' = y - (2x/y)
*/ 
double f(double x, double y){
    return y - (2 * x / y);
}
/**
* 求解析解
* @param x的值
* @return y的值 
*/
double f(double x){
    return sqrt(1 + 2 * x);
}
/**
* 二阶Runge-Kutta算法
* @param 初值x0, y0, 步长h, 迭代次数N
* @return void
*/ 
void rk2_1_2(double x0, double y0, const double h, const int N){
    printf("alpha_2 = 1/2\th=%f\n", h);
    printf("n\tx1\t\ty1\t\tf\t\terr\n");
    int n = 0;
    while(n != N){
        double x1 = x0 + h;
        double k1 = f(x0, y0);
        double k2 = f(x0 + 0.5 * h, y0 + 0.5 * h * k1);
        double y1 = y0 + h * k2;
        double _f = f(x1);
        double err = abs(y1 - _f);
        printf("%d\t%f\t%f\t%f\t%f\t\n", 
            n+1, x1, y1, _f, err);
        n++;
        y0 = y1, x0 = x1;
    }
}

int main(){
    const double x0 = 0, y0 = 1, h = 0.1, N = 10;    //初值、步长、迭代次数
    rk2_1_2(x0, y0, h, N);
    return 0;
}

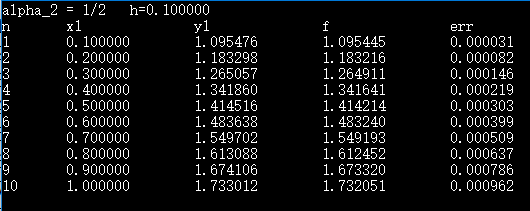
运行结果：