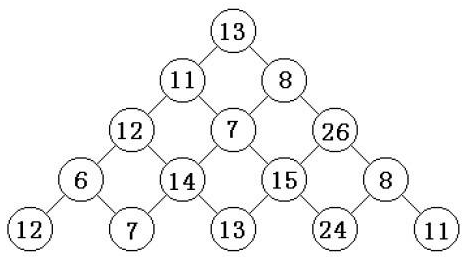
我们先看一个图片:
这是一个经典问题,图片上的东东是"数塔"。第一层有一个数字,第二层有两个数字。。。以此类推。
问题是,如果从第一层走到第n层(当然,不能走回头路),路径上的数字相加的最大和是多少呢?
如果从上到下考虑,可能并不是特别好分辨。13下面的路径有11和8,应当选比较大的11,而8下面有26,要比11下面的12大出一倍......所以我们最好 使用从下到上的思想。
在介绍这个思想之前先想个办法把这些数字按照它的结构保存起来。我们使用矩阵来存储这些数字:
f[1][1] = 13;
f[2][1] = 11, f[2][2] = 8;
f[3][1] = 12, f[3][2] = 7, f[3][3] = 26;
......接着我们从最下面的一层开始算,计算出每一个位置往下走所能收集到的最大数字之和。
第五行因为是最后一行,很显然往下走所能收集到的最大数字之和就是他们本身,我们将其保存起来
dp[5][1] = 12, dp[5][2] = 7, dp[5][3] = 13, dp[5][4] = 24, dp[5][5] = 11;接着我们计算第四行。第四行往下走的时候需要加上第5行所能走到的最大数字,我们得到了
dp[4][1] = f[4][1] + max(dp[5][1], dp[5][2]) = 6 + 12;
dp[4][2] = f[4][2] + max(dp[5][2], dp[5][3]) = 14 + 13;
......在第三行的计算中,我们同理,只需要加上每个数对应第四行所能达到的最大的数即可。这里不再敖述。
到了最后,计算到第一行,得到dp[1][1] = f[1][1] + max(dp[2][1], dp[2][2]);
这里dp[1][1]就是这里"从第一层走到第n层,路径上的数字相加最大"的结果了。
上面的算法中,每一次对当前位置的计算都是一次"决策",而dp[i][j]被称为问题的状态,上面计算dp[i][j]的式子称之为状态转移方程。
下面根据上面的思想给出动态规划的完整代码:
#include <iostream>
#include <algorithm>
using namespace std;
#define MAXN 1000
int main(){
int f[MAXN][MAXN]; //存放数塔
int dp[MAXN][MAXN]; //存放状态
int n;
printf("请输入要计算到第几层:");
scanf("%d", &n);
printf("请输入数塔:\n");
for(int i = 1; i <= n; i++){
for(int j = 1; j <= i; j++){
scanf("%d", &f[i][j]);
}
}
//计算最下面的一层
for(int i = 1; i <= n; i++){
dp[n][i] = f[n][i]; //最下面的一层dp都是自己本身
}
//从倒数第二层(n-1层)开始,向上计算dp[i][j]
for(int i = n-1; i >= 1; i--){
for(int j = 1; j <= i; j++){
//状态转移方程
dp[i][j] = max(dp[i+1][j], dp[i+1][j+1]) + f[i][j];
}
}
printf("%d\n", dp[1][1]);
return 0;
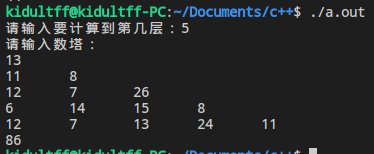
}输入前面提到的图中的数据,运行结果: