0x00、梗概
迪杰斯特拉(Dijkstra)算法是著名用来求最短路径的算法。被用于计算一个点到另一个点的最短路径。
其本质是贪心策略,主要思想和广度优先搜索(BFS)差不多,最大的特征是"层层遍历,直到终点"。
0x01、思路
Dijkstra算法是用来求图中某个顶点到另一个顶点的最短路径。这里的"最短"指代的不一定是"路程最短",而是边权累加之和最短。
使用Dijkstra算法计算时,思路如下:
-
指定起点s
-
定义两个集合:S和U,这里S用来记录已求出最短路径的途经顶点、以及相应最短路径的长度;U用来记录尚未求出最短路径的顶点、以及这个顶点到起点s的距离。
-
在初始时的状态:集合S中只包含起点s,集合U中包含除了起点s之外的所有顶点。
-
在Dijkstra执行的过程:{在U中找出路径最短的顶点 v,并将其加入到S中。接着更新U中的顶点。并以v为中介点,重新计算U中顶点到起点的距离,取最小值写入U }。接着再{从U中找出路径的顶点,加入到S中。并更新U中顶点,以及其所对应路径} 。。。。不断循环
-
直到遍历完全部顶点。
0x02、实现
我们举个实例帮助我们来讲解Dijkstra算法是如何实现的吧!
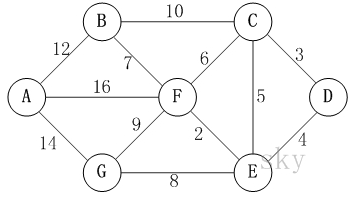
比如下面这个图
我们以D为起点举例。
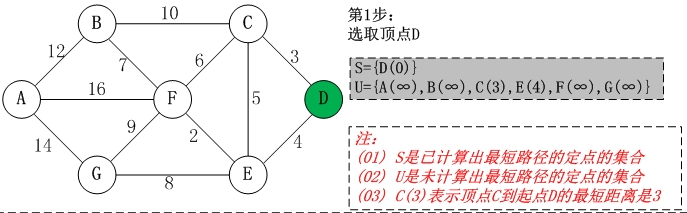
第一步:将起点D放入容器S,除了起点D之外的所有点放入容器U。
接着更新U容器内,各个顶点到D的距离。例如C到D距离为(C,D)=3,而F到D没有直达路线,(F,D)=INF(无穷大)
第二步:在U中,路径最小的是C,它到D的距离只有3。将C放入集合S中,同时将C从集合U中删除。
接着以C为中介点,更新U容器。B到D的距离为(B,C)+(C,D)=13,E到D的距离为(E,C)+(C,D)=8,而这个8大于数组原来的4,所以仍然取最小值4。F到D的距离为(F,C)+(C,D)=9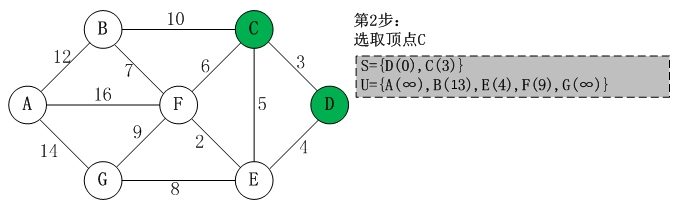
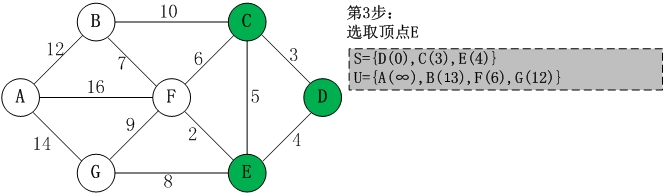
第三步:在U中,路径最小的是E,它到D的距离只有4。将E放入集合S中,同时将E从集合U中删除。
接着更新U容器。B到D的最短距离仍然是13,F到D的最短距离为(F,E)+(E,D)=6,G到D的最短距离为(G,E)+(E,D)=12
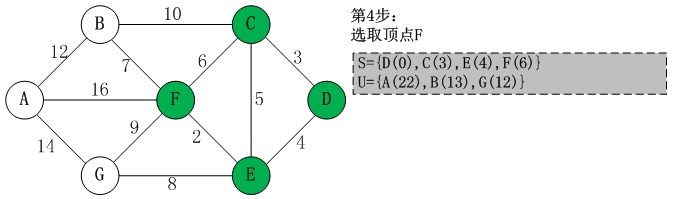
第四步:将最短的F放入S,并从U中删除。然后更新U
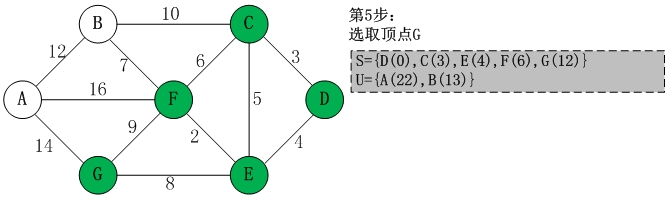
第五步:思路同上
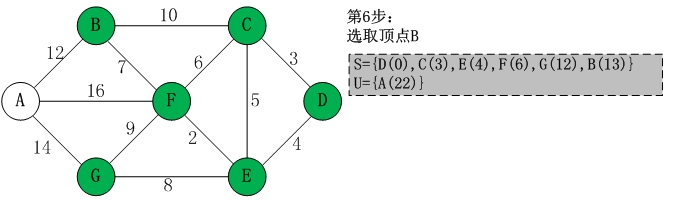
第六步:
第七步:将A放入S,集合U为空了。遍历结束。此时集合S中就是每个点到顶点D的最短边权值(最短路径)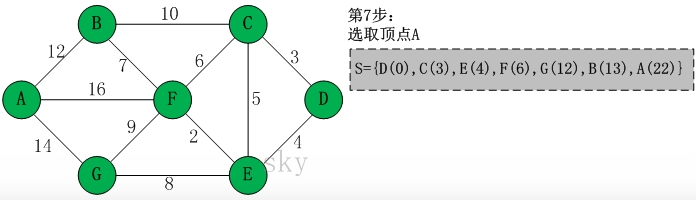
0x03、C语言实现
根据上面的思路先写出伪代码:
/* *
* Dijkstra
* G为图,d为数组,存放起点到各个点的最短路径长度,s是起点
*/
Dijkstra(G, d[], s){
初始化操作; //将d数组全部初始化为INF,令d[s]=0(起点到自身距离为0);
for(循环n次){ //其中n为顶点数,循环的目的是遍历所有点
u = 使得d[u]最小,且还没有被访问的顶点编号 //取出最小距离点
标记u为已访问 //防止重复遍历
for(从u出发能到达的所有顶点v){ //枚举更新
if(v尚未访问 && 以u为中介点,使得s到v的最短距离比已求出的d[v]更优){
更新d[v] //有更优路径,则更新
}
}
}
}在编写C语言代码之前,有两点注意:
-
前面说的"存放已经遍历过的节点的集合" S ,可以用一个bool型的数组 visited[ ] 来实现,visited[i] = true表示第 i 个节点已被访问,为false表示第 i 个节点尚未被访问。
-
那个非常大的数可以使用16进制数:0x3fffffff来表示。0x3fffffff=1073741823
图的存储可以使用邻接矩阵或者邻接表,我们依次编写。
先定义最大顶点数和INF:
#define MAXN 1000
#define INF 0x3fffffff1、邻接矩阵型
以下是邻接矩阵型的Dijkstra函数:
int n, G[MAXN][MAXN]; //n为顶点数,G为邻接矩阵
int d[MAXN]; //d数组存储起点到达各点最短路径长度
bool visited[MAXN] = {false}; //标记数组,前面说过了
/*Dijkstra算法。参数s为起点的编号*/
void Dijkstra(int s){
//下面两行为初始化操作
fill(d, d+MAXV, INF); //将数组d全部赋值为很大的数
d[s] = 0; //起点到自己本身的距离为0
for(int i = 0; i < n; i++){ //循环n次,n是顶点数,处理每一个点
int u = -1, MIN = INF; //u存放"用来找数组d中最小值的下标",MIN存放"数组d中的最小值"
for(int j = 0; j < n; j++){ //枚举每一个点
if(visited[j] == false) //如果这个点没有处理过
if(d[j] < MIN){ //并且这个点到顶点的距离比MIN小(MIN的初始值很大)
u = j; //让u等于最小值的下标
MIN = d[j]; //MIN等于d中的最小值
}
}
//如果u==-1,说明没有找到,也就是剩下的顶点与起点s不连通,我们直接终止函数
if(u == -1) return;
//如果找到了最小值的那个点,进行后续步骤
visited[u] = true; //标记这个点为已经访问过
for(int v = 0; v < n; v++){ //枚举每一个点
if(visited[v] == false) //如果这个点没有处理过
if(G[u][v] != INF) //如果刚刚那个最小值的点与这个点之间有路可走
if(d[u]+G[u][v]<d[v]) //如果以最小值点为中介点,到起点的距离小于之前算的起点的距离(如果之前没算过就是INF,一定成立)
d[v] = d[u] + G[u][v]; //更新d[v],使得d[v]最小
}
}
}以上就是邻接矩阵版的Dijkstra函数,下面我们尝试编写邻接表版。我们依然使用vector而不是链表来存储邻接表
2、邻接表型
typedef struct{
int v, dis; //v为边连接的目标顶点,dis为边权
} Node;
vector<Node> G[MAXN];
int n;
int d[MAXN];
bool visited[MAXN] = {false};
void Dijkstra(int s){ //s为起点
/*前面的所有写法与邻接矩阵版写法相同*/
//初始化操作
fill(d, d+MAXV, INF); //将数组d全部赋值为很大的数
d[s] = 0; //起点到自己本身的距离为0
for(int i = 0; i < n; i++){ //循环n次,n是顶点数,处理每一个点
int u = -1, MIN = INF; //u存放"用来找数组d中最小值的下标",MIN存放"数组d中的最小值"
for(int j = 0; j < n; j++){ //枚举每一个点
if(visited[j] == false) //如果这个点没有处理过
if(d[j] < MIN){ //并且这个点到顶点的距离比MIN小(MIN的初始值很大)
u = j; //让u等于最小值的下标
MIN = d[j]; //MIN等于d中的最小值
}
}
//如果u==-1,说明没有找到,也就是剩下的顶点与起点s不连通,我们直接终止函数
if(u == -1) return;
//如果找到了最小值的那个点,进行后续步骤
visited[u] = true; //标记这个点为已经访问过
/*仅此处的for循环与邻接矩阵版的写法不同*/
for(int j = 0; j < G[u].size; j++){ //枚举临街表中的所有顶点
int v = G[u][j].v; //此处可以通过临街表直接获得顶点。不用像邻接矩阵那样枚举
if(visited[v] == false) //如果这个点没有被访问过
if(d[u]+G[u][j].dis < d[v]) //并且边权和小于之前计算过的最短路径
d[v] = d[u] + G[u][j].dis; //更新最短路径
}
}
}对于多条最短路径、输出找到的路径,可以看这两篇哦: