图的遍历指的是:对图中所有顶点按照一定的顺序进行访问。访问的方法一般分为两种:DFS (深度优先) 和 BFS (广度优先) 。
0x00、深度优先搜索(DFS)遍历图的基本思路
深度优先,前面在走迷宫的那篇文章已经介绍过,特征是沿着一条路一直向前走。直到走到"死胡同",才返回最近的一条岔路口,再次往前走。直到走到终点。
举个栗子进行讲解吧:
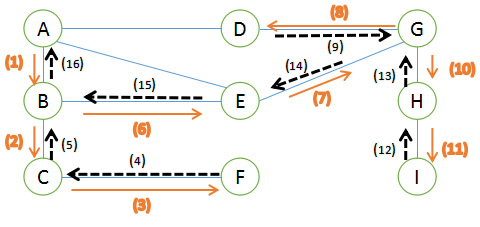
1-我们从A出发,将A输出,有B和D两种选择。此时的输出为A
1.1--我们选择B,将B输出,B是岔路口,有E和C两种选择。此时的输出为A、B
1.1.1---我们选择C,将C输出。此时的输出为A、B、C
1.1.2---C后面只有一条路,即F。我们到达了F,将F输出。此时输出为A、B、C、F
1.1.3---F是死胡同,返回到最近的一个岔路口:B。此时的输出为A、B、C、F
1.2--我们现在在B位置,B处有C和E两条路。我们刚刚选择了C,现在选择E
1.2.1---我们现在在E,将E输出。E后面只有一条路:G(因为A刚刚遍历过了,所以不遍历)此时的输出为ABCFE
1.2.2---我们到达了G。G是岔路口,我们先遍历D。此时的输出为ABCFEG
1.2.2.1----我们到了D,D是死胡同,返回G。此时的输出为ABCFEGD
1.2.3---我们回到了G,接着遍历H与I。I是死胡同,返回G。此时的输出为ABCFEGDHI
1.2.4---G的全部路径遍历完成,返回最近的岔路口E。E也遍历完成,返回B
1.3--B的全部遍历完成,返回A
2-A是起点。所以整张图遍历完成。最后的输出为A、B、C、F、E、G、D、H、I
路径就是橙色的线(去路)和黑色的虚线(归路)!
0x01、实现深度优先搜索遍历图的思想
在这个DFS算法的代码时,我们的思路是这样的:(这个是伪代码,仅仅代表思路,不可以执行)
DFS(Gid){ //Gid为图顶点号
printf Gid //访问这个节点
Visited[Gid] = true //设置该节点号已经访问过
for(当前节点出发所能到达的全部路径){ //枚举全部路径
if(Visited[New_Gid] == false){ //New_Gid为路径之一
DFS(New_Gid) //如果路径后的节点没有被访问过,就访问
}else continue; //如果访问过,则访问下一个节点
}
}这样就实现了对某个顶点以及 与它所连通的 全部顶点 的访问。
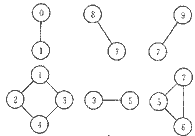
但是这里有个问题,比如下面这个图(忽略节点上的数字):
图中的顶点并不是全部连通的,我们使用DFS遍历的时候是无法全部遍历到的。所以我们还要写一个函数,让它能遍历所有的连通分量
DFSG(G){
for(G的所有顶点){
if(Visited[Gid] == false){
DFS(Gid);
}
}
}这样就能实现遍历整个图了。
上一篇文章写过遍历图的两种方法:邻接矩阵和邻接表。下面来写两个实例。
0x02、C语言实现DFS遍历图的实例
1、利用邻接矩阵:
const int INF = 1000000; //INF是一个很大的数,表示不存在
int n, G[1000][1000]; //n为图中顶点数,G为邻接矩阵
bool visited[1000] = {false}; //判断顶点是否访问过
void DFS(int u, int depth){ //u为当前访问的顶点号,depth为深度
visited[u] = true; //标记正在访问的节点为"已经访问过"
printf("%d", u); //输出这个节点
for(int i = 0; i < n; i++){ //枚举访问。i为下一个节点号
if(visited[i] == false && G[u][i] != INF){ //如果u和i之间有路径,且i没有被访问过
DFS(i, depth + 1); //则访问它
}
}
}
void DFSG(){ //遍历图的方法
for(int i = 0; i < n; i++){ //枚举所有顶点
if(visited[i] == false) //如果u没有被访问过
DFS(i, 1); //初次访问,深度为1
}
}2、利用邻接表
vector<int> Adj[1000]; //邻接表
int n; //n为顶点数
bool visited[1000] = {false}; //判断顶点是否访问过
void DFS(int u, int depth){
visited[u] = true;
printf("%d", u);
for(int i = 0; i < Adj[u].size(); i++){ //这里的i不再是下一节点号,而是用来枚举的临时变量
int v = Adj[u][i]; //v是邻接表中的下一节点号
if(visited[u] == false){
DFS(v, depth + 1);
}
}
}
void DFSG(){
for(int i= 0; i < n; i++){
if(visited[i] == false)
DFS(u, 1);
}
}0x03、广度优先搜索(BFS)遍历图的基本思路
广度优先搜索的特征为"广度",以扩散的形式访问顶点,层层遍历。
举个栗子:
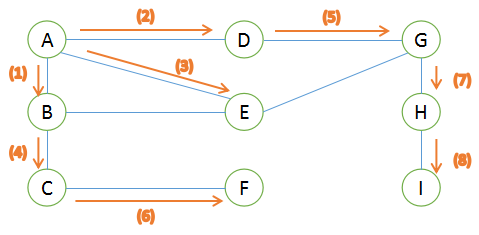
1-从起点A出发,A是岔路口,有两条路径B和D,B和D入队。此时队列为{B, D},输出为A
1.1--现在在队首B,B弹出队列,B是岔路口,C和E入队。此时队列为{D, C, E},输出为AB
1.2--现在队首为D,D弹出,D后面的路径只有G,G入队。此时队列为{C, E, G},输出为ABD
......(过程比较简单,不再重复)
直到所有元素处理完毕,队列为空,程序返回。
图中橙色路线即为遍历路径。
下面来用代码实现
0x04、实现广度优先搜索遍历图的思想
广度优先搜索的思想很容易理解,伪代码如下:
BFS(u){
queue Q;
u入队
visited[u] = true;
while(Q非空){
printf Q的队首
Q队首弹出
for(v in 从队首节点出发的所有可能){
if(visited[v] == false){
v入队
visited[v] = true; //标记顶点u为"已遍历过"
}
}
}
}同样,这样的代码只能处理一个连通分量,为了遍历可能包含多个连通分量的图,我们需要对图中的所有顶点进行判断
BFSG(){
for(u in 所有顶点){
if(visited[u] == false)
BFS(u);
}
}这样就是完整的思路,下面我们来把它分邻接表和邻接矩阵两种情况,分别写成代码。
0x05、C语言实现BFS遍历图的实例
1、利用邻接矩阵
int n, G[1000][1000];
bool visited[1000] = {false};
void BFS(u){
queue<int> Q;
Q.push(u);
visited[u] = true;
while(!Q.empty()){
int u = Q.front();
Q.pop();
for(int v = 0; v < n; v++){ //枚举所有路径
if(visited[v] == false && G[u][v] != INF){ //u到v的路径存在并且v没有被访问过
Q.push(v);
visited[v] = true;
}
}
}
}
void BFSG(){
for(int u = 0; u < n; u++)
if(visited[u] == false)
BFS(u);
}2、利用邻接矩阵
vector<int> Adj(1000);
int n;
bool visited[1000] = {false};
void BFS(u){
queue<int> Q;
Q.push(u);
visited[u] = true;
while(!Q.empty()){
int u = Q.front();
Q.pop();
for(int i = 0; i < Adj[u].size(); i++){
int v = Adj[u][i];
if(visited[v] == false){
Q.push(v);
visited[v] = true;
}
}
}
}
void BFSG(){
for(int u = 0; u < n; u++)
if(visited[u] == false)
BFS(u);
}0x06、带有层号信息的BFS遍历
在某种特殊的情况下,我们有时需要使得遍历带有层级信息,这种情况我们只需要对邻接表的结构进行修改,并对BFS方法稍作修改即可
首先修改邻接表的结构
typedef struct{
int v; //顶点编号
int layer; //本顶点的层号
} Node;
vector<Node> Adj(N)这样,属性为vector的Adj表就带有了层号信息,下面我们让BFS函数遍历时对每个节点都加上层号
void BFS(int s){ //s为起点编号
queue<Node> Q;
Node start; //start在这里充当记录起始节点的临时变量
start.v = s;
start.layer = 0; //起始层号为0
Q.push(start); //压入队列
while(!Q.empty()){
Node top = Q.front(); //记录队首节点的临时变量
Q.pop();
int u = node.v; //这里u是记录队首节点的节点编号
for(int i = 0; i < Adj[u].size(); i++){
Node next = Adj[u][i]; //next为u能到达的下一个节点
next.layer = top.layer + 1; //另下一层级的层号等于当前顶点层号+1
if(visited[next.v] == false){
Q.push(next);
visited[next.v] = true;
}
}
}
}