在解Dijkstra的问题时,常常会遇到最短路径不止一条的情况。就像这样:
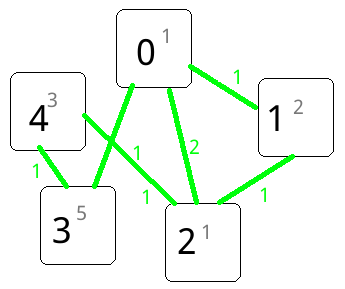
图中绿色为边,绿色字体为边权,灰色字体为点权,黑色字体为顶点编号。
如果我们计算从0到2的最短路径,答案是有两条,0--1--2和0--2
0、出题套路
在考察这类问题时,通常分三种情况:
-
给每条边在第一边权的基础上增加一个边权,即"第二边权",要求在第一边权最短的情况下,让第二边权最短(或最大)。
例如:第一边权是距离,第二边权是路费。要求在距离最短的情况下求出路费最短的路径
-
给每一个点加一个点权(就像上面给出的图那样),要求在边权最短的情况下让点权之和最大(或最小)
例如:边权是距离,点权是到达城市能收集到的物资。要求路径最短的情况下收集到的物资最多
-
直接问有多少条最短路径
对于这三种出题方法,只需要增加一个数组存放新增边权或点权或最短路径条数。然后在之前发表的文章"最短路径 - 迪杰斯特拉(Dijkstra)算法详解"的代码中,对寻找最小值的循环稍作修改即可
下面均以邻接矩阵为例。邻接表的情况可以自行修改。
1、新增边权
例如原来的边权表示距离,新增的边权表示路费。假设s是起点,我们定义一个二维数组:cost[u][v] 表示 顶点u->顶点v 的消费(这个一定是题目给出的),接着增加一个数组 c[u],表示起点s到顶点u的最少消费。初始化的时候令c[s]=0,这是因为起点到自己本身是不需要消费的。数组c的其余值都是INF,在每次找最小点的时候更新数组c的值,就可以达到寻找最少消费的目的。
代码如下:
/*@@@@@@@ 以下都是原来的代码,不需要修改 @@@@@@@*/
int n, G[MAXN][MAXN]; //n为顶点数,G为邻接矩阵
int d[MAXN]; //d数组存储起点到达各点最短路径长度
bool visited[MAXN] = {false}; //标记数组,前面说过了
/*Dijkstra算法。s为起点的编号*/
void Dijkstra(int s){
fill(d, d+MAXV, INF); //将数组d全部赋值为很大的数
d[s] = 0; //起点到自己本身的距离为0
for(int i = 0; i < n; i++){ //循环n次,n是顶点数,处理每一个点
int u = -1, MIN = INF; //u存放"用来找数组d中最小值的下标",MIN存放"数组d中的最小值"
for(int j = 0; j < n; j++){ //枚举每一个点
if(visited[j] == false) //如果这个点没有处理过
if(d[j] < MIN){ //并且这个点到顶点的距离比MIN小(MIN的初始值很大)
u = j; //让u等于最小值的下标
MIN = d[j]; //MIN等于d中的最小值
}
}
//如果u==-1,说明没有找到,也就是剩下的顶点与起点s不连通,我们直接终止函数
if(u == -1) return;
//如果找到了最小值的那个点,进行后续步骤
visited[u] = true; //标记这个点为已经访问过
for(int v = 0; v < n; v++){ //枚举每一个点
/*@@@@@@@ 这个循环的里面需要进行修改,加上计算路费的代码 @@@@@@@*/
if(visited[v] == false && G[u][v] != INF){ //如果这个点没有处理过,且有路可走
if(d[u]+G[u][v]<d[v]){ //如果以最小值点为中介点可以找到更短路径
c[v] = c[u] + cost[u][v]; //更新到达v的消费 = 到达u的消费 + u和v之间的路费
d[v] = d[u] + G[u][v]; //更新d[v],使得d[v]最小
}else if(d[u] + G[u][v] == d[v] && c[u] + cost[u][v] < c[v]){
//以最小值点为中介点的路径与之前找到的最短路径相同,但是路费却更少的情况
c[v] = c[u] + cost[u][v]; //更新到达v的消费 = 到达u的消费 + u和v之间的路费
}
}
/*@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@*/
}
}
}我们在更新最短路径的时候,同时更新了所需路费。如果最短路径相同的时候,我们判断了路费的解是否最优。在路径不是最短的时候,直接忽略,这是因为一切大前提是路径最短。一切都必须确保路径是最短的,在这个基础上才可以考虑费用等其他的。
如果题目要求计算第二边权最大,只需要将"c[u] + cost[u][v] < c[v]"这一句的"<"改为">"
2、新增点权
例如原来边权表示距离,新增点权表示城市中能收集到的物资数量。使用数组 weight[u] 表示点u的点权(题目给出),并新增一个用来记录数据w[u],表示起点s到顶点u可以收集到的最大物资量。初始化的时候只有w[s]和weight[s](题目给出),其余w[]均为0。和上面增加边权的方式一样,我们仍然在老位置修改代码:
/*@@@@@@@ 以下都是原来的代码,不需要修改 @@@@@@@*/
int n, G[MAXN][MAXN]; //n为顶点数,G为邻接矩阵
int d[MAXN]; //d数组存储起点到达各点最短路径长度
bool visited[MAXN] = {false}; //标记数组,前面说过了
/*Dijkstra算法。s为起点的编号*/
void Dijkstra(int s){
fill(d, d+MAXV, INF); //将数组d全部赋值为很大的数
d[s] = 0; //起点到自己本身的距离为0
for(int i = 0; i < n; i++){ //循环n次,n是顶点数,处理每一个点
int u = -1, MIN = INF; //u存放"用来找数组d中最小值的下标",MIN存放"数组d中的最小值"
for(int j = 0; j < n; j++){ //枚举每一个点
if(visited[j] == false) //如果这个点没有处理过
if(d[j] < MIN){ //并且这个点到顶点的距离比MIN小(MIN的初始值很大)
u = j; //让u等于最小值的下标
MIN = d[j]; //MIN等于d中的最小值
}
}
//如果u==-1,说明没有找到,也就是剩下的顶点与起点s不连通,我们直接终止函数
if(u == -1) return;
//如果找到了最小值的那个点,进行后续步骤
visited[u] = true; //标记这个点为已经访问过
for(int v = 0; v < n; v++){ //枚举每一个点
/*@@@@@@@ 这个循环的里面需要进行修改,加上计算物资量的代码 @@@@@@@*/
if(visited[v] == false && G[u][v] != INF){ //如果这个点没有处理过,且有路可走
if(d[u]+G[u][v]<d[v]){ //如果以最小值点为中介点可以找到更短路径
w[v] = w[u] + weight[v]; //更新到达v积累的物资 = 到达u积累的物资 + 在v处能积累下的物资
d[v] = d[u] + G[u][v]; //更新d[v],使得d[v]最小
}else if(d[u] + G[u][v] == d[v] && w[u] + weight[v] > w[v]){
//以最小值点为中介点的路径与之前找到的最短路径相同,但是路费却更少的情况
w[v] = w[u] + weight[v]; //更新到达v积累的物资 = 到达u积累的物资 + 在v处能积累下的物资
}
}
/*@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@*/
}
}
}如果题目要求计算点权最小,只需要将"w[u] + weight[v] > w[v]"这一句的">"改为"<"
3、计算最短路径条数
这种题目更好办,直接在有相同路径长度的判断上加一个累加计数器即可。
当发现新的最短路径时,说明当前层的最短路径只有这一条,我们只需要继承上一级的最短路径条数。
当发现有最短路径与上一级的路径长度相同时,说明这一层最短路径不知这一条,我么要进行累加。
我们定义一个数组num[u]表示起点s到顶点u的最短路径条数。在起始状态,num[s]=1,num数组其他的值全部为0,接着还是在老地方,修改代码:
/*@@@@@@@ 以下都是原来的代码,不需要修改 @@@@@@@*/
int n, G[MAXN][MAXN]; //n为顶点数,G为邻接矩阵
int d[MAXN]; //d数组存储起点到达各点最短路径长度
bool visited[MAXN] = {false}; //标记数组,前面说过了
/*Dijkstra算法。s为起点的编号*/
void Dijkstra(int s){
fill(d, d+MAXV, INF); //将数组d全部赋值为很大的数
d[s] = 0; //起点到自己本身的距离为0
for(int i = 0; i < n; i++){ //循环n次,n是顶点数,处理每一个点
int u = -1, MIN = INF; //u存放"用来找数组d中最小值的下标",MIN存放"数组d中的最小值"
for(int j = 0; j < n; j++){ //枚举每一个点
if(visited[j] == false) //如果这个点没有处理过
if(d[j] < MIN){ //并且这个点到顶点的距离比MIN小(MIN的初始值很大)
u = j; //让u等于最小值的下标
MIN = d[j]; //MIN等于d中的最小值
}
}
//如果u==-1,说明没有找到,也就是剩下的顶点与起点s不连通,我们直接终止函数
if(u == -1) return;
//如果找到了最小值的那个点,进行后续步骤
visited[u] = true; //标记这个点为已经访问过
for(int v = 0; v < n; v++){ //枚举每一个点
/*@@@@@@@ 这个循环的里面需要进行修改,加上计算物资量的代码 @@@@@@@*/
if(visited[v] == false && G[u][v] != INF){ //如果这个点没有处理过,且有路可走
if(d[u]+G[u][v]<d[v]){ //如果以最小值点为中介点可以找到更短路径
d[v] = d[u] + G[u][v]; //更新d[v],使得d[v]最小
num[v] = num[u]; //如果走到了这个if里面,说明这个岔路口只有这一种最短路径。继承之前路径数即可
}else if(d[u] + G[u][v] == d[v]){//如果最短距离相同
num[v] += num[u]; //执行累加
}
}
/*@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@*/
}
}
}4、更变态的情况(三种情况叠加)
假如出题老师非常非常厉害,上面三种情况包含了两种,甚至三种都包含了!
怎么办!
还是老地方,多加个判断语句就行了!
还是不会?做为一个良心博主,继续给你举例子:
例如要求在路径最短的情况下,找出点权最大的情况,同时求出最短路径条数。
老地方,把for语句里面的 if语句 改成这个样子:
if(visited[v] == false && G[u][v] != INF){ //如果这个点没有处理过,且有路可走
if(d[u]+G[u][v]<d[v]){ //如果以最小值点为中介点可以找到更短路径
d[v] = d[u] + G[u][v]; //更新d[v],使得d[v]最小
num[v] = num[u]; //继承之前路径数
w[v] = w[u] + weight[v]; //更新点权
}else if(d[u] + G[u][v] == d[v]){//如果最短距离相同
num[v] += num[u]; //执行累加
if(w[u] + weight[v] > w[v]){
w[v] = w[u] + weight[v]; //更新总点权
}
}
}

非常感谢大佬的总结,对我真的有很大的帮助,谢谢!