记忆化搜索--优化斐波那契数列递归函数

记忆化搜索，即在搜索过程中记录下搜索结果，在下次的搜索过程中如果算出过这个结果，就可以直接拿来用。

举个栗子：

现有一个问题，要求写出一个函数，功能是输出第n个斐波那契数列。

斐波那契数列是这样的：1,1,2,3,5,8......

直接的办法是开一个数组，计算斐波那契数列到第n个，然后输出array[n]就可以了

int f(int n){
    int fibo[MAXN] = {0,1};
    for(int i = 2; i <= n; i++)
        fibo[i] = fibo[i-2] + fibo[i-1];
    return fibo[n];
}

现在要求：必须使用递归！

问题还是很简单。斐波那契数列的递归定义为：F(0)=0，F(1)=1, F(n)=F(n-1)+F(n-2)（n>=2，n∈N*），根据这一定义即可写出程序：

int f(int n){
    if(n == 0 || n == 1) return 1;    //递归终点
    else return f(n-1) + f(n-2);
}

但是这里有个问题。比如n=5，递归式中需要计算f(4)和f(3)，而计算f(4)的时候又需要计算f(3)和f(2)，这就产生了计算重复，使得时间复杂度达到指数级别O(2ⁿ)

为了避免重复计算，我们需要新开一个数组来保存计算后的结果

int dp[MAXN] = {0};

int f(int n){
    if(n == 0 || n == 1) return 1;    //递归边界
    if(dp[n] == 0)
        dp[n] = f(n-1) + f(n-2);    //如果没有计算过，计算它
    //如果计算过，就不用算了
    //最后都返回dp[n]
    return dp[n];
}

这样可以大大的降低时间复杂度，降至O(n)

来写个程序看看运行耗时吧！

#include <stdio.h>
#include <time.h>
#define MAXN 100

int dp[MAXN] = {0};

int f1(int n){
    if(n == 0 || n == 1) return 1;    //递归边界
    if(dp[n] == 0)
        dp[n] = f1(n-1) + f1(n-2);    //如果没有计算过，计算它
    //如果计算过，就不用算了
    //最后都返回dp[n]
    return dp[n];
}

int f2(int n){
    if(n == 0 || n == 1) return 1;    //递归终点
    else return f2(n-1) + f2(n-2);
}

int main(){
    int n;
    clock_t start, stop;
    scanf("%d", &n);
    start = clock();
    printf("%d\n", f2(n));
    stop = clock();
    printf("f2耗时：%.0fms\n", double((stop-start) * 1000 / CLOCKS_PER_SEC));
    start = clock();
    printf("%d\n", f1(n));
    stop = clock();
    printf("f1耗时：%.0fms\n", double((stop-start) * 1000 / CLOCKS_PER_SEC));
    return 0;
}

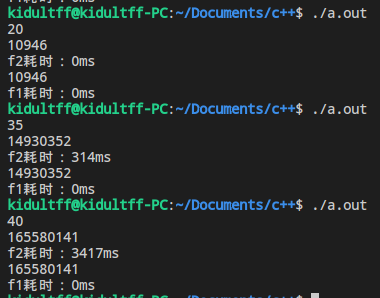
运行结果：