PAT-A 真题 – 1131 Subway Map

In the big cities, the subway systems always look so complex to the visitors. To give you some sense, the following figure shows the map of Beijing subway. Now you are supposed to help people with your computer skills! Given the starting position of your user, your task is to find the quickest way to his/her destination.

Input Specification:

Each input file contains one test case. For each case, the first line contains a positive integer $N$ ( $\leq$ 100), the number of subway lines. Then $N$ lines follow, with the $i$ -th ( $i = 1, \dots, N$ ) line describes the $i$ -th subway line in the format:

$M$ S[1] S[2] ... S[ $M$ ]

where $M$ ( $\leq$ 100) is the number of stops, and S[ $i$ ]'s ( $i = 1, \dots, M$ ) are the indices of the stations (the indices are 4-digit numbers from 0000 to 9999) along the line. It is guaranteed that the stations are given in the correct order -- that is, the train travels between S[ $i$ ] and S[ $i + 1$ ] ( $i = 1, \dots, M - 1$ ) without any stop.

Note: It is possible to have loops, but not self-loop (no train starts from S and stops at S without passing through another station). Each station interval belongs to a unique subway line. Although the lines may cross each other at some stations (so called "transfer stations"), no station can be the conjunction of more than 5 lines.

After the description of the subway, another positive integer $K$ ( $\leq$ 10) is given. Then $K$ lines follow, each gives a query from your user: the two indices as the starting station and the destination, respectively.

The following figure shows the sample map.

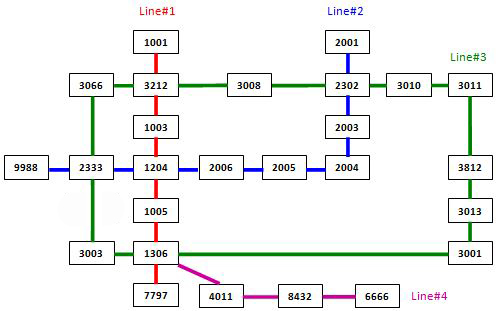
Note: It is guaranteed that all the stations are reachable, and all the queries consist of legal station numbers.

Output Specification:

For each query, first print in a line the minimum number of stops. Then you are supposed to show the optimal path in a friendly format as the following:

Take Line#X1 from S1 to S2.
Take Line#X2 from S2 to S3.
......

where X $i$ 's are the line numbers and S $i$ 's are the station indices. Note: Besides the starting and ending stations, only the transfer stations shall be printed.

If the quickest path is not unique, output the one with the minimum number of transfers, which is guaranteed to be unique.

Sample Input:

4
7 1001 3212 1003 1204 1005 1306 7797
9 9988 2333 1204 2006 2005 2004 2003 2302 2001
13 3011 3812 3013 3001 1306 3003 2333 3066 3212 3008 2302 3010 3011
4 6666 8432 4011 1306
3
3011 3013
6666 2001
2004 3001

Sample Output:

2
Take Line#3 from 3011 to 3013.
10
Take Line#4 from 6666 to 1306.
Take Line#3 from 1306 to 2302.
Take Line#2 from 2302 to 2001.
6
Take Line#2 from 2004 to 1204.
Take Line#1 from 1204 to 1306.
Take Line#3 from 1306 to 3001.

题目大意：给出地铁每一条线的经停站，之后给出起点和终点，要求找到经停站最少的路线，如果存在多条，找到换乘次数最少的路线。

这道题是一道图的遍历问题，DFS算法没什么难度，难点在于如何计算换乘了几次。

一种很笨但是很直接的办法是，保存每个经停站都属于哪些路线，然后根据前后站点一个个计算，但是这样写起来特别麻烦，还容易出错，时间复杂度也接近O(2n²)

另外一种办法是用矩阵存储每个站点到下一个站点的路线属于哪一条地铁线，但是0000-9999意味着你要开10000*10000=100000000大小的数组，这也太夸张了吧...内存超限妥妥的

用map存储，你需要这么定义：map<pair<int, int>, int>，前一个pair存放两个经停站，后面的int存放属于哪条线路，这看起来也很麻烦的。

一个比较好的办法是用8位数存储，前四位是起点，后四位是终点，思想有点类似哈希映射，那么映射的函数就是：起点*10000 + 终点

有了这个思想，很容易就写出来了~

#include <iostream>
#include <bits/stdc++.h>
using namespace std;

const size_t maxn = 10010;
vector<int>  G[maxn],  //邻接表
      road,    //路径
      tmp;    //临时路径
map<int, int> T;    //存储路线 
int start, fin;      //起点、终点 
int MinTransfer = 0x7fffffff;//最小换乘次数 
bool v[maxn];

int Hash(int start, int end){
  return start * 10000 + end;
}

int TransCnt(){
  int cnt = 0, _line = T[Hash(tmp[0], tmp[1])];
  for(int i = 1; i < tmp.size(); i++){
    int h = Hash(tmp[i-1], tmp[i]);
    if(T[h] != _line){
      _line = T[h];
      cnt++;
    }
  }
  return cnt;
}

void init(){
  MinTransfer = 0x7fffffff;
  road.clear();
  tmp.clear();
  fill(v, v + maxn, false);
}

void dfs(int s){
  tmp.push_back(s);
  v[s] = true;
  if(s == fin){  //到达终点
    int trans = TransCnt();
    if(  (road.size() == 0 || tmp.size() < road.size()) ||   //第一次找到路或找到经停站更少的 
      (tmp.size() == road.size() && trans < MinTransfer)){//经停站一样多，但是换乘次数更少 
      MinTransfer = trans;
      road = tmp;
    }
  }
  else{
    for(auto i : G[s])
      if(v[i] == false) dfs(i);
  }
  v[s] = false;
  tmp.pop_back(); 
}

int main(){
  int Lcnt, Qcnt;
  cin >> Lcnt;
  //读入邻接表 
  for(int i = 1; i <= Lcnt; i++){
    int cnt, _1, _2;
    cin >> cnt >> _1; 
    for(int j = 1; j < cnt; j++){
      cin >> _2;
      T[10000*_1+_2] = T[10000*_2+_1] = i;  //记录路线 
      G[_1].push_back(_2);  //无向图邻接表
      G[_2].push_back(_1);
      _1 = _2;
    }
  }
  cin >> Qcnt;
  for(int i = 0; i < Qcnt; i++){
    init();
    cin >> start >> fin;
    dfs(start);
    cout << road.size() - 1 << endl;
    //计算乘的第一条地铁线
    int _line = T[Hash(road[0], road[1])];
    printf("Take Line#%d from %04d to ", _line, road[0]);
    for(int _ = 1; _ < road.size(); _++){
      if(T[Hash(road[_], road[_-1])] != _line){
        printf("%04d.\n", road[_-1]);
        _line = T[Hash(road[_], road[_-1])];
        printf("Take Line#%d from %04d to ", _line, road[_-1]);
      }
    }
    //计算最后一个
    printf("%04d.\n", fin);
  }
  return 0;
}

斐斐のBlog